题目内容
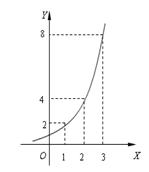
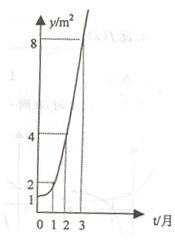 如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间(月)的关系:y=ax(a>0且a≠1),有以下叙述:
如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间(月)的关系:y=ax(a>0且a≠1),有以下叙述:①这个指数函数的底数是2;
②第5个月时,浮萍的面积就会超过30m2;
③若浮萍蔓延到2m2、3m2、6m2所经过的时间分别为t1、t2、t3,则t1+t2=t3,其中正确的序号是
分析:本题考查的是函数模型的选择和应用问题.在解答时,首先应该仔细观察图形,结合图形读出过的定点进而确定函数解析式,结合所给月份计算函数值从而获得相应浮萍的面积进而对问题作出判断,至于第③要充分结合对数运算的运算法则进行计算验证.
解答:解:由题意可知:浮萍蔓延的面积(m2)与时间(月)的关系:y=ax(a>0且a≠1),且由函数图象可知函数过点(1,2),
∴a1=2,∴a=2,∴这个指数函数的底数是2正确;
∴函数的解析式为:y=2x,
所以当x=5 时,y=25=32>30,故第5个月时,浮萍的面积就会超过30m2成立;
对③由于:2=2t1,3=2t2,6=2t3,
∴t1=1,t2=log23,t3=log26,
又因为1+log23=log22+log23=log22×3=log26,
∴若浮萍蔓延到2m2、3m2、6m2所经过的时间分别为t1、t2、t3,则t1+t2=t3成立.
故答案为:①②③.
∴a1=2,∴a=2,∴这个指数函数的底数是2正确;
∴函数的解析式为:y=2x,
所以当x=5 时,y=25=32>30,故第5个月时,浮萍的面积就会超过30m2成立;
对③由于:2=2t1,3=2t2,6=2t3,
∴t1=1,t2=log23,t3=log26,
又因为1+log23=log22+log23=log22×3=log26,
∴若浮萍蔓延到2m2、3m2、6m2所经过的时间分别为t1、t2、t3,则t1+t2=t3成立.
故答案为:①②③.
点评:本题考查的是函数模型的选择和应用问题.在解答的过程当中充分体现了观察图形、分析图形和利用图形的能力,同时对数求值和对数运算的能力也得到了体现,值得同学们体会与反思.

练习册系列答案
相关题目
 10、如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间t(月)的关系:y=at,有以下叙述:
10、如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间t(月)的关系:y=at,有以下叙述: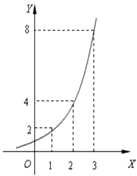 如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间x(月)的关系:y=ax,有以下叙述:
如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间x(月)的关系:y=ax,有以下叙述: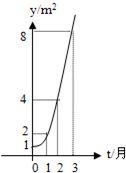 20、如图所示的是某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系:y=at,请解决以下问题:
20、如图所示的是某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系:y=at,请解决以下问题: 与时间
与时间 (月)的关系:
(月)的关系: ,有以下叙述:① 这个指数函数的底数是2;②第5个月的浮萍的面积就会超过
,有以下叙述:① 这个指数函数的底数是2;②第5个月的浮萍的面积就会超过 ;③浮萍从
;③浮萍从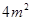 蔓延到
蔓延到 需要经过1.5个月;④浮萍每个月增加的面积都相等;⑤若浮萍蔓延到
需要经过1.5个月;④浮萍每个月增加的面积都相等;⑤若浮萍蔓延到 、
、 、
、 所经过的时间分别为
所经过的时间分别为 ,则
,则 .其中正确的是( )
.其中正确的是( )