题目内容
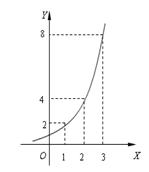
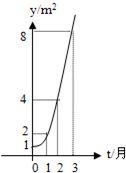 20、如图所示的是某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系:y=at,请解决以下问题:
20、如图所示的是某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系:y=at,请解决以下问题:①求出这个指数函数的表达式;
②求第5个月时浮萍的面积;
③浮萍从4m2蔓延到16m2恰好要经过多少个月.
分析:(1)由已知中函数的图象,我们易判断指数函数经过(1,2)点,代入函数的解析式,即可求出底数a,进而即可求出这个指数函数的表达式;
(2)将t=5代入函数的解析式,即可求出第5个月时浮萍的面积;
(3)分别将y=4m2,y=16m2分别代入函数解析式,求出对应的t值,即可得到浮萍从4m2蔓延到16m2恰好要经过多少个月.
(2)将t=5代入函数的解析式,即可求出第5个月时浮萍的面积;
(3)分别将y=4m2,y=16m2分别代入函数解析式,求出对应的t值,即可得到浮萍从4m2蔓延到16m2恰好要经过多少个月.
解答:解:(1)由图可知当t=1时,y=2
代入y=at,易得a=2
故这个指数函数的表达式为y=2t,
(2)当t=5时
y=25=32
即第5个月时浮萍的面积为32m2
(3)当y=4m2时,
4=2t,解得t=2
当y=16m2时,
16=2t,解得t=4
故浮萍从4m2蔓延到16m2恰好要经过2个月
代入y=at,易得a=2
故这个指数函数的表达式为y=2t,
(2)当t=5时
y=25=32
即第5个月时浮萍的面积为32m2
(3)当y=4m2时,
4=2t,解得t=2
当y=16m2时,
16=2t,解得t=4
故浮萍从4m2蔓延到16m2恰好要经过2个月
点评:本题考查的知识点是指数函数的综合应用,其中根据图象,确定函数图象经过的点的坐标,求出函数的解析式是解答本题的关键.

练习册系列答案
相关题目
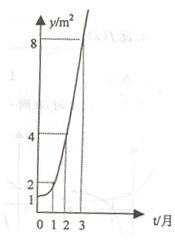 如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间(月)的关系:y=ax(a>0且a≠1),有以下叙述:
如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间(月)的关系:y=ax(a>0且a≠1),有以下叙述: 10、如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间t(月)的关系:y=at,有以下叙述:
10、如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间t(月)的关系:y=at,有以下叙述: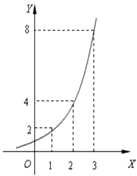 如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间x(月)的关系:y=ax,有以下叙述:
如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间x(月)的关系:y=ax,有以下叙述: 与时间
与时间 (月)的关系:
(月)的关系: ,有以下叙述:① 这个指数函数的底数是2;②第5个月的浮萍的面积就会超过
,有以下叙述:① 这个指数函数的底数是2;②第5个月的浮萍的面积就会超过 ;③浮萍从
;③浮萍从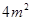 蔓延到
蔓延到 需要经过1.5个月;④浮萍每个月增加的面积都相等;⑤若浮萍蔓延到
需要经过1.5个月;④浮萍每个月增加的面积都相等;⑤若浮萍蔓延到 、
、 、
、 所经过的时间分别为
所经过的时间分别为 ,则
,则 .其中正确的是( )
.其中正确的是( )