摘要：设f(x)是定义在R上的偶函数.其图象关于直线x=1对称.对任意x1.x2∈［0.］都有f(x1+x2)=f(x1)·f(x2). 且f(1)=a＞0. (1)求f()及f() 是周期函数, (3)记an=f(2n+.求an. (1)解 ∵对x1.x2∈. 都有f(x1+x2)=f(x1)·f(x2). ∴f(x)=f(≥0.x∈［0.1］. ∴f(1)=f( f(. ∵f(1)=a＞0, ∴f 的图象关于直线x=1对称. ∴f=f(2-x).x∈R. 又由f=f(x).x∈R. ∴f.x∈R. 将上式中-x用x代换.得f.x∈R. 这表明f(x)是R上的周期函数.且2是它的一个周期. ≥0.x∈［0.1］. ∵f(=f(- =f(-·f(又f( ∵f(x)的一个周期是2.∴an=f(2n+)=f(),∴an=a.
网址：http://m.1010jiajiao.com/timu_id_4463441[举报]
设f(x)是定义在R上的偶函数，其图象关于直线x=1对称，对任意x1,x2∈［0，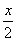
］都有f(x1+x2)=f(x1)·f(x2).
］都有f(x1+x2)=f(x1)·f(x2).(1)设f(1)=2,求f(
),f(
);
(2)证明f(x)是周期函数.
查看习题详情和答案>>设f(x)是定义在R上的偶函数，其图象关于直线x=1对称，对任意x1、x2∈［0,
］,都有f(x1+x2)=f(x1)·f(x2),且f(1)=a>0.
(1)求f()、f(
);
(2)证明f(x)是周期函数；
查看习题详情和答案>>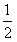
］,都有f(x1+x2)=f(x1)·f(x2),且f(1)=a>0. 
);
),求
]，都有
。
； 
］,都有f(x1+x2)=f(x1)·f(x2).
),f(
);