题目内容
设f(x)是定义在R上的偶函数，其图象关于x=1对称，对任意x1，x2∈[0，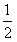
]，都有
。
（1）设f(1)=2，求
；
（2）证明f(x)为周期函数。
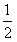]，都有。（1）设f(1)=2，求
； （2）证明f(x)为周期函数。
（1）解：由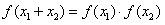
，
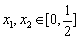知，
，
∵
，
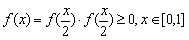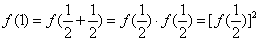又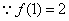
，
∴
，
，
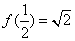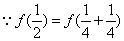
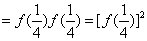又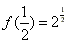
，
∴
。
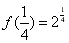（2）证明：依题意，设y=f（x）关于直线x=1对称，f（x）=f（2-x），x∈R，
又∵f（x）为偶函数，
∴f（-x）=f（x），x∈R，f（-x）= f（2-x），
以-x代x有f（x）=f（2+x），x∈R，
这说明f（x）是R上的周期函数，且2是它的周期。
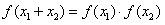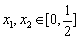，知，，∵
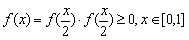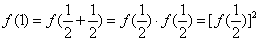，又
，∴
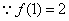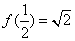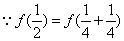
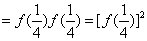，，又
，∴
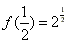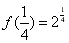。（2）证明：依题意，设y=f（x）关于直线x=1对称，f（x）=f（2-x），x∈R，
又∵f（x）为偶函数，
∴f（-x）=f（x），x∈R，f（-x）= f（2-x），
以-x代x有f（x）=f（2+x），x∈R，
这说明f（x）是R上的周期函数，且2是它的周期。
练习册系列答案
相关题目
]都有f (x1＋x2) = f (x1) ? f (x2)．且f (1) = a＞0．
)；
)，求
．
f(0n)(1-x)n+
f(
)x(1-x)n-1+…+
f(
)xn(1-x)0(x≠0,1).
,又当-3≤x≤-2时，f(x)=2x,则f(113.5)的值是（ ）
B.-
C.
D.-
)x－1，若在区间(－2，6]内关于x的方程f(x)－loga(x＋2)＝0(a＞1)恰有3个不同的实数根，则a的取值范围是
) D. (