摘要:7.质量为m的小球固定在光滑轻细杆的上端.细杆通过光滑限位孔保持竖直.在光滑水平面上放置一质量为M=2m的凹形槽.凹形槽的光滑内表面如图所示.AB部分是斜面.与水平面成θ=30°.BCD部分是半径为R的圆弧面.AB与BCD两面在B处相切.让细杆的下端与凹形槽口的左边缘A点接触.现将小球释放.求: (1)当轻细杆的下端滑到凹形槽的最低点C时. 凹形槽的速度是多大, (2)轻细杆的下端能否运动到凹形槽口的右边缘 D点,(只要回答“能 或“不能 .不需说明原因) (3)当轻细杆的下端滑到B点的瞬间.小球和凹形槽的速度各是多大. 答案:(1)当轻细杆的下端运动到最低点C时.小球的速度为零.小球减少的重力势能转化为凹形槽的动能.由能量转化守恒定律 又 M=2m 得凹形槽的速度: (2)能. (3)当轻细杆的下端从A点相对滑动到B点时. 小球的速度v1与凹形槽的速度v2之间的关系如右图所示:得: 由系统能量转化守恒定律 又 M=2m 解得:
网址:http://m.1010jiajiao.com/timu_id_4463277[举报]
(06年广东卷)(15分)(1)人们发现光电效应具有瞬时性和对各种金属都存在极限频率的规律。请问谁提出了何种学说很好地解释了上述规律?已知锌的逸出功为3.34e,用某单色紫外线照射锌板时,逸出光电子的最大速度为106m/s,求该紫外线的波长λ(电子质量me=9.11×![]() kg
kg![]() J?s,1eV=1.6×10
J?s,1eV=1.6×10![]() J)。
J)。
(2)风力发电是一种环保的电能获取方式。图9为某风力发电站外观图。设计每台风力发电机的功率为40kW。实验测得风的动能转化为电能的效率约为20%,空气的密度是1.29kg/m3,当地水平风速约为10m/s,问风力发电机的叶片长度约为多少才能满足设计要求?
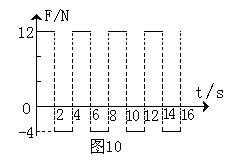
查看习题详情和答案>>(06年广东卷)(14分)一个质量为![]() 的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数
的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数![]() 。从
。从![]() 开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图10所示。求83秒内物体的位移大小和力F对物体所做的功。
开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图10所示。求83秒内物体的位移大小和力F对物体所做的功。![]() 取
取![]() 。
。
(06年广东卷)(16分)宇宙中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其它星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个项点上,并沿外接于等边三角形的圆形轨道运行。设每个星体的质量均为![]() 。
。
(1)试求第一种形式下,星体运动的线速度和周期。
(2)假设两种形式星体的运动周期相同,第二种形式下星体之间的距离应为多少?
查看习题详情和答案>>