摘要:抽象函数的性质所对应的一些具体特殊函数模型: ①正比例函数 ②,指数函数, ③,对数函数, 课本题1.设集合..则集合{且}=[1,3].
网址:http://m.1010jiajiao.com/timu_id_4463020[举报]
已知函数f(x)=sinπx的图象的一部分如下方左图,则下方右图的函数图象所对应的函数解析式为( )
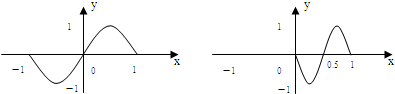
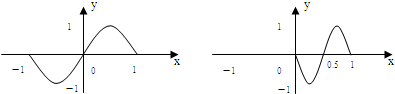
A、y=f(2x-
| ||||
| B、y=f(2x-1) | ||||
C、y=f(
| ||||
D、y=f(
|
在学习二项式定理时,我们知道杨辉三角中的数具有两个性质:①每一行中的二项式系数是“对称”的,即第1项与最后一项的二项式系数相等,第2项与倒数第2项的二项式系数相等,…;②图中每行两端都是1,而且除1以外的每一个数都等于它肩上两个数的和.我们也知道,性质①对应于组合数的一个性质:cnm=Cnn-m.
(1)试写出性质②所对应的组合数的另一个性质;
(2)请利用组合数的计算公式对(1)中组合数的另一个性质作出证明.
查看习题详情和答案>>
(1)试写出性质②所对应的组合数的另一个性质;
(2)请利用组合数的计算公式对(1)中组合数的另一个性质作出证明.
 如图,是一位骑自行车和一位骑摩托车在相距80km的两城间行驶的函数图象;其中骑自行车用了6小时(含途中休息1小时),骑摩托车用了2小时.
如图,是一位骑自行车和一位骑摩托车在相距80km的两城间行驶的函数图象;其中骑自行车用了6小时(含途中休息1小时),骑摩托车用了2小时.(1)有人根据这个图象,提出关于两人的信息如下:
①骑自行车比骑摩托车早出发3小时,晚到2小时;
②骑自行车是变速运动,骑摩托车是匀速运动;
③骑摩托车在出发1.5小时后追上骑自行车的,其中正确的序号为?
(2)设骑自行车和骑摩托车的人所对应函数分别为f(x),g(x);求f(x),g(x)解析式,并写出定义域;
(3)定义函数?(x)=g(
| x2-2x+a | 40 |
 (2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.
(2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.(1)写出m的值并求出当0≤x≤m时,点P运动路径的长度l;
(2)写出函数f(x),x∈[4k-2,4k+2],k∈Z的表达式;研究该函数的性质并填写下面表格:
| 函数性质 | 结 论 | |
| 奇偶性 | 偶函数 偶函数 | |
| 单调性 | 递增区间 | [4k,4k+2],k∈z [4k,4k+2],k∈z |
| 递减区间 | [4k-2,4k],k∈z [4k-2,4k],k∈z | |
| 零点 | x=4k,k∈z x=4k,k∈z | |