题目内容
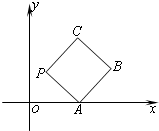（2012•浦东新区一模）如图所示，在平面直角坐标系xOy上放置一个边长为1的正方形PABC，此正方形PABC沿x轴滚动（向左或向右均可），滚动开始时，点P位于原点处，设顶点P（x，y）的纵坐标与横坐标的函数关系是y=f（x），x∈R，该函数相邻两个零点之间的距离为m．（1）写出m的值并求出当0≤x≤m时，点P运动路径的长度l；
（2）写出函数f（x），x∈[4k-2，4k+2]，k∈Z的表达式；研究该函数的性质并填写下面表格：
| 函数性质 | 结 论 | |
| 奇偶性 | 偶函数 偶函数 | |
| 单调性 | 递增区间 | [4k，4k+2]，k∈z [4k，4k+2]，k∈z |
| 递减区间 | [4k-2，4k]，k∈z [4k-2，4k]，k∈z | |
| 零点 | x=4k，k∈z x=4k，k∈z | |
分析：（1）m即正方形的周长，l由3段
圆弧构成，其中2段弧所在圆的半径等于1，1段弧所在圆的半径等于
，从而
求得l的值．
（2）用分段函数表示函数f（x）的解析式，由此求出递增区间和递减区间，及函数的零点．
（3）易知直线y=ax恒过原点，函数y=f（x），x∈[-8，8]的图象关于y轴对称，分类讨论直线y=ax在每一段上
与y=f（x）的交点的个数，综合可得结论．
| 1 |
| 4 |
| 2 |
求得l的值．
（2）用分段函数表示函数f（x）的解析式，由此求出递增区间和递减区间，及函数的零点．
（3）易知直线y=ax恒过原点，函数y=f（x），x∈[-8，8]的图象关于y轴对称，分类讨论直线y=ax在每一段上
与y=f（x）的交点的个数，综合可得结论．
解答：解：（1）m即正方形的周长，∴m=4，…（2分）
l由3段
圆弧构成，其中2段弧所在圆的半径等于1，1段弧所在圆的半径等于
，
故l=2[
×2π×1]+
×2π×
=（1+
）π．…（4分）
（2）函数f（x）=
，k∈z．…（7分）
…（10分）
（3）f（x）=a|x|在区间[-8，8]删的根的个数即为函数f（x）的图象和直线y=a|x|的交点个数，
（i）易知直线y=ax恒过原点；
当直线y=ax过点（1，1）时，a=1，此时点（2，0）到直线y=x的距离为
，
直线y=x与曲线 y=
，x∈[1，3]相切．
当x≥3时，y=x恒在曲线y=f（x）之上．
（ii）当直线y=ax与曲线 y=
，x∈[5，7]相切时，由点（6，0）到直线y=ax
的距离为
，a=
，此时点（5，0）到直线 y=
x的距离为
，
直线y=
x与曲线y=
，x∈[4，5]相离．
（iii）当直线y=ax与曲线 y=
，x∈[4，5]相切时，由点（5，0）到直线 y=ax
的距离为1，a=
=
，此时点（6，0）到直线y=
x的距离为
＜
，
直线y=
x与曲线 y=
，x∈[5，7]相交于两个点．
（ⅳ）当直线y=ax过点（5，1）时，a=
，此时点（5，0）到直线y=
x的距离为
＜1，直线y=
x与曲线 y=
，x∈[4，5]相交于两个点．
点（6，0）到直线y=
x的距离为
＜
，直线y=
x与曲线y=
，x∈[5，7]相交于两个点．
（ⅴ）当a=0时，直线y=0与曲线y=f（x），x∈[-8，8]有且只有5个交点；
（ⅵ）当a＜0时，直线y=ax与曲线y=f（x），x∈[-8，8]有且只有1个交点；
因为函数y=f（x），x∈[-8，8]的图象关于y轴对称，…（14分）
故综上可知：（1）当a＜0时，方程 f（x）=a|x|只有1实数根；
（2）当a＞
时，方程f（x）=a|x|有3个实数根；
（3）当a=
，或a=0时，方程f（x）=a|x|有5个实数根；
（4）当 0＜a＜
或
＜a＜
时，方程f（x）=a|x|有7个实数根；
（5）当a=
时，方程f（x）=a|x|有9个实数根；
（6）当a=
，方程f（x）=a|x|有2个实数根；
（7）当
＜a＜
时，方程f（x）=a|x|有11个实数根．…（18分）
l由3段
| 1 |
| 4 |
| 2 |
故l=2[
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| ||
| 2 |
（2）函数f（x）=
|
| 函数性质 | 结 论 | |
| 奇偶性 | 偶函数 | |
| 单调性 | 递增区间 | [4k，4k+2]，k∈z |
| 递减区间 | [4k-2，4k]，k∈z | |
| 零点 | x=4k，k∈z | |
（3）f（x）=a|x|在区间[-8，8]删的根的个数即为函数f（x）的图象和直线y=a|x|的交点个数，
（i）易知直线y=ax恒过原点；
当直线y=ax过点（1，1）时，a=1，此时点（2，0）到直线y=x的距离为
| 2 |
直线y=x与曲线 y=
| 2-(x-2)2 |
当x≥3时，y=x恒在曲线y=f（x）之上．
（ii）当直线y=ax与曲线 y=
| 2-(x-6)2 |
的距离为
| 2 |
| 1 | ||
|
| 1 | ||
|
| 5 | ||
|
直线y=
| 1 | ||
|
| 1-(x-5)2 |
（iii）当直线y=ax与曲线 y=
| 1-(x-5)2 |
的距离为1，a=
| 1 | ||
|
| ||
| 12 |
| 1 | ||
|
| 6 | ||
|
| 2 |
直线y=
| 1 | ||
|
| 2-(x-6)2 |
（ⅳ）当直线y=ax过点（5，1）时，a=
| 1 |
| 5 |
| 1 |
| 5 |
| 5 | ||
|
| 1 |
| 5 |
| 1-(x-5)2 |
点（6，0）到直线y=
| 1 |
| 5 |
| 6 | ||
|
| 2 |
| 1 |
| 5 |
| 2-(x-6)2 |
（ⅴ）当a=0时，直线y=0与曲线y=f（x），x∈[-8，8]有且只有5个交点；
（ⅵ）当a＜0时，直线y=ax与曲线y=f（x），x∈[-8，8]有且只有1个交点；
因为函数y=f（x），x∈[-8，8]的图象关于y轴对称，…（14分）
故综上可知：（1）当a＜0时，方程 f（x）=a|x|只有1实数根；
（2）当a＞
| ||
| 17 |
（3）当a=
| ||
| 17 |
（4）当 0＜a＜
| 1 |
| 5 |
| ||
| 12 |
| ||
| 17 |
（5）当a=
| ||
| 12 |
（6）当a=
| 1 |
| 5 |
（7）当
| 1 |
| 5 |
| ||
| 12 |
点评：本题主要考查分段函数的应用，体现了分类讨论的数学思想，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
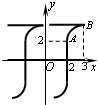（2012•浦东新区二模）手机产业的发展催生了网络新字“孖”．某学生准备在计算机上作出其对应的图象，其中A（2，2），如图所示．在作曲线段AB时，该学生想把函数