摘要：11．＝x2+2mx+2m+3的零点为x1.x2.求x12+x22的最小值． [解析] 由题意知.方程x2+2mx+2m+3＝0的两个根为x1.x2.则 ∴x12+x22＝(x1+x2)2-2x1x2＝4m2-2 ＝4m2-4m-6 ＝42-7. ∵Δ≥0.∴4m2-4≥0. ∴m2-2m-3≥0.∴m≤-1.或m≥3. ∴当m＝-1时.x12+x22取最小值2.
网址：http://m.1010jiajiao.com/timu_id_4462264[举报]
（本题满分15分）
已知函数f (x )=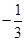
ax
3 + x2 + 2 ( a ≠ 0 ) ．
(Ⅰ) 试讨论函数f (x )的单调性；
(Ⅱ) 若a>0，求函数f (x ) 在［1，2］上的最大值．
查看习题详情和答案>>
（本小题15分）已知函数f(x)=(1+x)2-aln(1+x)2在(-2,-1)上是增函数，
在（-∞，-2）上为减函数.
（1）求f(x)的表达式；
（2）若当x∈
时，不等式f(x)＜m恒成立，求实数m的值；
（3）是否存在实数b使得关于x的方程f(x)=x2+x+b在区间［0，2］上恰好有两个相异的实根，若存在，求实数b的取值范围.
查看习题详情和答案>>
（本小题满分15分）
已知函数f(x)＝－1＋2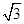
sinxcosx＋2cos2x.
(1)求f(x)的单调递减区间；
(2)求f(x)图象上与原点最近的对称中心的坐标；
(3)若角α，β的终边不共线，且f(α)＝f(β)，求tan(α＋β)的值．
查看习题详情和答案>>
，直线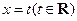
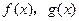的图象分别交于M、N两点．
时，求｜MN｜的值；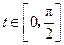
时的最大值．
（
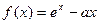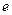为自然对数的底数）．a
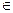R
1）当a=1时,求函数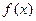
的最小值；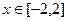
上存在极小值，求a的取值范围；
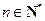，证明：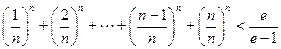
．