题目内容
(本题满分15分)
已知函数f (x )=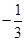 ax
3 + x2 + 2 ( a ≠ 0 ) .
ax
3 + x2 + 2 ( a ≠ 0 ) .
(Ⅰ) 试讨论函数f (x )的单调性;
(Ⅱ) 若a>0,求函数f (x ) 在[1,2]上的最大值.
解: (1) ①当a>0时, f(x)在(-∞,0),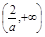 上是减函数,在
上是减函数,在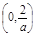 上是增函数.
上是增函数.
②当a<0时, f(x)在(-∞, 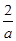 ),(0, +∞)上是增函数,在(
),(0, +∞)上是增函数,在(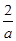 ,0)上是减函数.
,0)上是减函数.
(2)当0<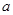 <1时,f(x)的最大值为3-
<1时,f(x)的最大值为3-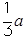 ,
,
当1≤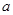 ≤2时,f(x)的最大值为
≤2时,f(x)的最大值为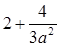 ,
,
当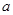 >2时,f(x)的最大值为
>2时,f(x)的最大值为 .
.
【解析】本试题主要是考查了函数单调性和函数最值的求解的综合运用。
(1)根据已知条件,对于参数a进行分类讨论,判定单调性得到结论。
(2)在第一问的基础上,进一步对于不同情况下的单调性分别研究得到最值。
选做题:(参加IB学习的学生必须做,不参加IB学习的学生原则上不要做)
题目:(本题满分值为10分)
解: (1)
∵f(x)=- ax3+x2+2
(a≠0),∴
ax3+x2+2
(a≠0),∴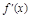 = -ax2+2x.
= -ax2+2x.
①当a>0时,令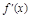 >0,即-ax2+2x>0,得0<x<
>0,即-ax2+2x>0,得0<x<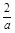 .
.
∴f(x)在(-∞,0),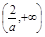 上是减函数,在
上是减函数,在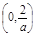 上是增函数. ………………4分
上是增函数. ………………4分
②当a<0时,令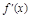 >0,即-ax2+2x>0,得x>0,或x<
>0,即-ax2+2x>0,得x>0,或x<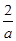 .
.
∴f(x)在(-∞, 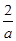 ),(0, +∞)上是增函数,在(
),(0, +∞)上是增函数,在(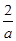 ,0)上是减函数.………………8分
,0)上是减函数.………………8分
(2)由(1)得:
①当0<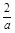 <1,即a>2时,f(x)在(1,2)上是减函数,
<1,即a>2时,f(x)在(1,2)上是减函数,
∴f(x)max=f(1)=3-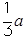 . ……………10分
. ……………10分
②当1≤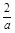 ≤2,即1≤a≤2时,f(x)在
≤2,即1≤a≤2时,f(x)在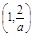 上是增函数,在
上是增函数,在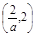 上是减函数,
上是减函数,
∴f(x)max=f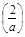 =
=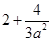 .
………12分
.
………12分
③当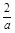 >2时,即0<
>2时,即0<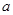 <1时,f(x)在(1,2)上是增函数,
<1时,f(x)在(1,2)上是增函数,
∴f(x)max=f(2)=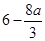 .
……………14分
.
……………14分
综上所述,当0<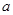 <1时,f(x)的最大值为3-
<1时,f(x)的最大值为3-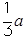 ,
,
当1≤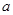 ≤2时,f(x)的最大值为
≤2时,f(x)的最大值为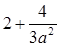 ,
,
当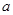 >2时,f(x)的最大值为
>2时,f(x)的最大值为 . ………………15分
. ………………15分

 .
. 在
在 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数 的最大值;
的最大值; 对任意的
对任意的 ,
, 都成立,求实数
都成立,求实数 的取值范围.
的取值范围. 为自然对数的底数.
为自然对数的底数. 与曲线
与曲线 相切
相切 在
在 上恰有两个不等的实数根
上恰有两个不等的实数根 ,求
,求 的大小
的大小 :
: (
( ),焦点为
),焦点为 ,直线
,直线 交抛物线
交抛物线 、
、 两点,
两点, 是线段
是线段 的中点,
的中点, 轴的垂线交抛物线
轴的垂线交抛物线 ,
, 到焦点
到焦点 ,求此时
,求此时 的值;
的值; 是以
是以

 的单调区间;
的单调区间; ,若
,若 在
在 上不单调且仅在
上不单调且仅在 处取得最大值,求
处取得最大值,求 的取值范围.
的取值范围.