题目内容
(本小题满分15分)
已知函数f(x)=-1+2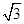 sinxcosx+2cos2x.
sinxcosx+2cos2x.
(1)求f(x)的单调递减区间;
(2)求f(x)图象上与原点最近的对称中心的坐标;
(3)若角α,β的终边不共线,且f(α)=f(β),求tan(α+β)的值.
【答案】
(1) [kπ+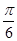 ,kπ+
,kπ+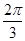 ](k∈Z)
;(2) (-
](k∈Z)
;(2) (- ,0) ;(3)
,0) ;(3) 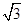 .
.
【解析】
试题分析:f(x)=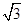 sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+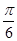 ),
),
(1)由2kπ+ ≤2x+
≤2x+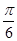 ≤2kπ+
≤2kπ+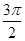 (k∈Z)
(k∈Z)
得kπ+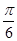 ≤x≤kπ+
≤x≤kπ+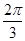 (k∈Z),
(k∈Z),
∴f(x)的单调递减区间为[kπ+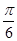 ,kπ+
,kπ+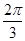 ](k∈Z)
](k∈Z)
(2)由sin(2x+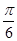 )=0得2x+
)=0得2x+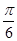 =kπ(k∈Z),
=kπ(k∈Z),
即x=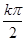 -
- (k∈Z),
(k∈Z),
∴f(x)图象上与原点最近的对称中心的坐标是(- ,0).
,0).
(3)由f(α)=f(β)得:
2sin(2α+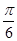 )=2sin(2β+
)=2sin(2β+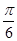 ),
),
又∵角α与β的终边不共线,
∴(2α+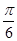 )+(2β+
)+(2β+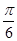 )=2kπ+π(k∈Z),
)=2kπ+π(k∈Z),
即α+β=kπ+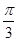 (k∈Z),∴tan(α+β)=
(k∈Z),∴tan(α+β)=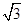 .
.
考点:二倍角公式;和差公式;三角函数的性质。
点评:求函数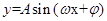 的单调区间,一定要注意
的单调区间,一定要注意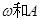 的正负,此为易错点,也是常考点。此题属于基础题型。
的正负,此为易错点,也是常考点。此题属于基础题型。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的单调区间;
的单调区间; ,试分别解答以下两小题.
,试分别解答以下两小题. 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 是两个不相等的正数,且
是两个不相等的正数,且 ,求证:
,求证: .
. 、
、 分别为椭圆
分别为椭圆 :
: 的
的  :
: 的焦点,
的焦点, 是
是 。
。 :
: ,过点P的动直线
,过点P的动直线 与圆
与圆 ,
, (
( 且
且 )。求证:点Q总在某定直线上。
)。求证:点Q总在某定直线上。
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,过
,过 与椭圆相交于A、B两点。
与椭圆相交于A、B两点。 ,且
,且 ,求椭圆的离心率;
,求椭圆的离心率; 求
求 的最大值和最小值。
的最大值和最小值。
 在定义域内存在区间
在定义域内存在区间 ,满足
,满足 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出 ;若不是,说明理由;
;若不是,说明理由; 为“优美函数”,求实数
为“优美函数”,求实数 的取值范围.
的取值范围.