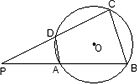
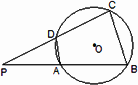
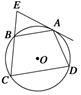
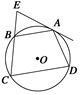
摘要：5．如图.四边形ABCD内接于⊙O.＝. 过A点的切线交CB的延长线于E点． 求证:AB2＝BE·CD. 证明:连结AC.因为EA切⊙O于A. 所以∠EAB＝∠ACB. 因为＝. 所以∠ACD＝∠ACB.AB＝AD. 于是∠EAB＝∠ACD. 又四边形ABCD内接于⊙O.所以∠ABE＝∠D. 所以△ABE∽△CDA. 于是＝.即AB·DA＝BE·CD. 所以AB2＝BE·CD.

网址：http://m.1010jiajiao.com/timu_id_4461699[举报]