题目内容
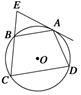
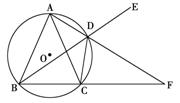
(本小题12分)如图,四边形ABCD内接于⊙O,AB=AD过A点的切线交CB的延长线于E点.求证:AB2=BE·CD.
【答案】
见解析.
【解析】利用连结AC.∵EA切⊙O于A,∴∠EAB=∠ACB,
∵AB=AD,∴∠ACD=∠ACB,AB=AD.∴∠EAB=∠ACD.
又四边形ABCD内接于⊙O,所以∠ABE=∠D.
∴△ABE∽△CDA.
∴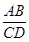 =
=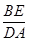 ,即AB·DA=BE·CD.
,即AB·DA=BE·CD.
∴AB2=BE·CD
证明 连结AC.
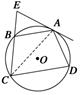
∵EA切⊙O于A,∴∠EAB=∠ACB,
∵AB=AD,
∴∠ACD=∠ACB,AB=AD.
∴∠EAB=∠ACD.
又四边形ABCD内接于⊙O,
所以∠ABE=∠D.
∴△ABE∽△CDA.
∴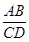 =
=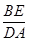 ,即AB·DA=BE·CD.
,即AB·DA=BE·CD.
∴AB2=BE·CD.

练习册系列答案
相关题目
 中,AC=BC, AC⊥BC,点D是A1B1中点.
中,AC=BC, AC⊥BC,点D是A1B1中点.  ,求二面角D- AC1-A1的余弦值.
,求二面角D- AC1-A1的余弦值.
 中,
中, 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是 的菱形,
的菱形, 为
为 的中点.
的中点. 与底面
与底面 平面
平面 ;
; 的余弦值.
的余弦值. 
 中,底面
中,底面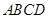 是正方形,
是正方形, ,
,  底面
底面 分别在
分别在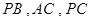 上,且
上,且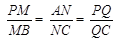
 ∥平面
∥平面 .
. 与平面面
与平面面

 平面BCD;
平面BCD;