题目内容
如图所示,已知四边形ABCD内接于⊙O,∠C=130°,AD是⊙O的直径,过B作⊙O的切线FE,求∠ABE的度数.
140°
解析解 因为四边形ABCD为⊙O的内接四边形,∠C=130°,所以∠A=50°.
连接OB,则∠ABO=50°,所以∠AOB=80°.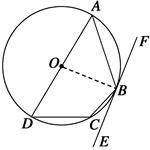
又因为∠ABF=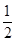 ∠AOB=40°,
∠AOB=40°,
所以∠ABE=180°-∠ABF=180°-40°=140°,
即∠ABE=140°.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目





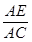 的值;
的值;
 上的点(不与点A,C重合),延长BD至E.
上的点(不与点A,C重合),延长BD至E.
 ,求△ABC外接圆的面积.
,求△ABC外接圆的面积.