摘要： 教材加强了函数与信息技术整合的要求.通过电脑绘制简单函数动态图象,使学生初步感受到信息技术在函数学习中的重要作用.
网址：http://m.1010jiajiao.com/timu_id_4460072[举报]
，
的图像分别与
轴、
轴交于
、
两点，且
，函数
. 当
时，求函数
的最小值.[
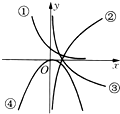如图给出了函数y=ax，y=logax，y=log（a+1）x，y=（a-1）x2的图象，则与函数y=ax，y=logax，y=log（a+1）x，y=（a-1）x2依次对应的图象是（ ）
查看习题详情和答案>>
定义：若函数f（x）的图象经过变换T后所得图象对应的函数与f（x）的值域相同，则称变换T是f（x）的同值变换．下面给出了四个函数与对应的变换：
（1）f（x）=（x-1）2，T1将函数f（x）的图象关于y轴对称；
（2）f（x）=2x-1-1，T2将函数f（x）的图象关于x轴对称；
（3）f（x）=
，T3将函数f（x）的图象关于点（-1，1）对称；
（4）f（x）=sin（x+
），T4将函数f（x）的图象关于点（-1，0）对称．
其中T是f（x）的同值变换的有
查看习题详情和答案>>
（1）f（x）=（x-1）2，T1将函数f（x）的图象关于y轴对称；
（2）f（x）=2x-1-1，T2将函数f（x）的图象关于x轴对称；
（3）f（x）=
| x |
| x+1 |
（4）f（x）=sin（x+
| π |
| 3 |
其中T是f（x）的同值变换的有
（1）（3）（4）
（1）（3）（4）
．（写出所有符合题意的序号）
某种商品的成本为5元/件，开始按8元/件销售，销售量为50件，为了获取最大利润，商家先后采取了提价与降价两种措施进行试销．经试销发现：销售价每上涨1元每天销售量就减少10件；而降价后，日销售量Q（件）与实际销售价x（元）满足关系Q=
（1）求总利润（利润=销售额-成本）y（元）与实际销售价x（件）的函数关系式；
（2）试问：当实际销售价为多少元时，总利润最大． 查看习题详情和答案>>
|
（1）求总利润（利润=销售额-成本）y（元）与实际销售价x（件）的函数关系式；
（2）试问：当实际销售价为多少元时，总利润最大． 查看习题详情和答案>>
（本小题满分14分）某种商品的成本为5元/ 件，开始按8元/件销售，销售量为50件，为了获得最大利润，商家先后采取了提价与降价两种措施进行试销。经试销发现：销售价每上涨1元每天销售量就减少10件；而降价后，日销售量Q（件）与实际销售价x（元）满足关系：
|
[
[
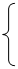
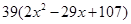
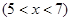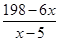
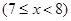（1）求总利润（利润＝销售额－成本）y（元）与销售价x（件）的函数关系式；
（2）试问：当实际销售价为多少元时，总利润最大.
查看习题详情和答案>>