题目内容
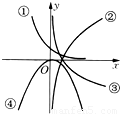
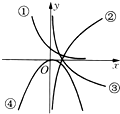 如图给出了函数y=ax,y=logax,y=log(a+1)x,y=(a-1)x2的图象,则与函数y=ax,y=logax,y=log(a+1)x,y=(a-1)x2依次对应的图象是( )
如图给出了函数y=ax,y=logax,y=log(a+1)x,y=(a-1)x2的图象,则与函数y=ax,y=logax,y=log(a+1)x,y=(a-1)x2依次对应的图象是( )分析:由二次函数的图象为突破口,根据二次函数的图象开口向下得到a的范围,然后由指数函数和对数函数的图象的单调性得答案.
解答:解:由图象可知y=(a-1)x2为二次函数,且图中的抛物线开口向下,
∴a-1<0,即a<1.
又指数函数和对数函数的底数大于0且不等于1,
∴y=ax为减函数,图象为①;y=logax为减函数,图象为③;y=log(a+1)x为增函数,图象为②.
∴与函数y=ax,y=logax,y=log(a+1)x,y=(a-1)x2依次对应的图象是①③②④.
故选B.
∴a-1<0,即a<1.
又指数函数和对数函数的底数大于0且不等于1,
∴y=ax为减函数,图象为①;y=logax为减函数,图象为③;y=log(a+1)x为增函数,图象为②.
∴与函数y=ax,y=logax,y=log(a+1)x,y=(a-1)x2依次对应的图象是①③②④.
故选B.
点评:本题考查了基本初等函数的图象和性质,是基础的概念题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
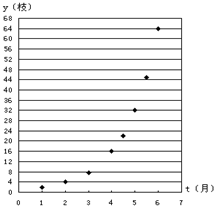 9、如图给出了红豆生长时间t(月)与枝数y(枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好?( )
9、如图给出了红豆生长时间t(月)与枝数y(枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好?( )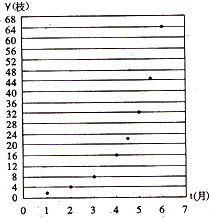 (2012•宝鸡模拟)如图给出了一种植物生长时间t(月)与枝数y(枝)之间的散点图.请你根据此判断这种植物生长的时间与枝数的关系用下列哪个函数模型拟合最好?( )
(2012•宝鸡模拟)如图给出了一种植物生长时间t(月)与枝数y(枝)之间的散点图.请你根据此判断这种植物生长的时间与枝数的关系用下列哪个函数模型拟合最好?( )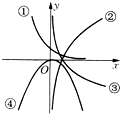 如图给出了函数y=ax,y=logax,y=log(a+1)x,y=(a-1)x2的图象,则与函数y=ax,y=logax,y=log(a+1)x,y=(a-1)x2依次对应的图象是
如图给出了函数y=ax,y=logax,y=log(a+1)x,y=(a-1)x2的图象,则与函数y=ax,y=logax,y=log(a+1)x,y=(a-1)x2依次对应的图象是