摘要：原函数在区间上单调递增.则一定存在反函数.且反函数也单调递增,但一个函数存在反函数.此函数不一定单调．判断一个函数的奇偶性时.你注意到函数的定义域是否关于原点对称这个必要非充分条件了吗?特例:
网址：http://m.1010jiajiao.com/timu_id_4458403[举报]
给出下列说法：①幂函数的图象一定不过第四象限；②奇函数图象一定过坐标原点；③ 
的递增区间为
；④定义在R上的函数
对任意两个不等实数a、b,总有
成立，则在R上是增函数；⑤
的单调减区间是
;正确的有____________
查看习题详情和答案>>
给出下列说法：①幂函数的图象一定不过第四象限；②奇函数图象一定过坐标原点；③ 
的递增区间为
；④定义在R上的函数
对任意两个不等实数a、b,总有
成立，则在R上是增函数；⑤
的单调减区间是
;正确的有____________
给出下列说法：①幂函数的图象一定不过第四象限；②奇函数图象一定过坐标原点；③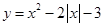 
的递增区间为
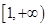；④定义在R上的函数
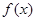对任意两个不等实数a、b,总有
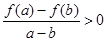成立，则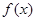在R上是增函数；⑤
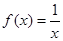的单调减区间是
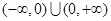;正确的有____________
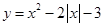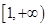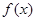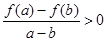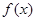的递增区间为；④定义在R上的函数对任意两个不等实数a、b,总有成立，则在R上是增函数；⑤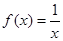的单调减区间是;正确的有____________
＞0成立，则f(x)在R上是增函数；⑤f(x)＝
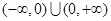的单调减区间是(－∞，0)∪(0，＋∞)；正确的有________．