题目内容
给出下列说法:①幂函数的图象一定不过第四象限;②奇函数图象一定过坐标原点;③  的递增区间为
的递增区间为 ;④定义在R上的函数
;④定义在R上的函数 对任意两个不等实数a、b,总有
对任意两个不等实数a、b,总有 成立,则
成立,则 在R上是增函数;⑤
在R上是增函数;⑤ 的单调减区间是
的单调减区间是 ;正确的有____________
;正确的有____________
【答案】
①④
【解析】
试题分析:①因为x>0时,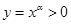 ,所以幂函数的图象一定不过第四象限.正确;
,所以幂函数的图象一定不过第四象限.正确;
②因为定义域不一定包括0,所以奇函数图象不一定过坐标原点.错;
③因为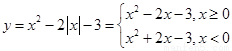 ,所以
,所以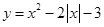 的递增区间为
的递增区间为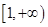 和
和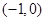 ,错;
,错;
④因为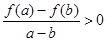 ,所以
,所以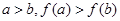 ,根据增函数的定义可知此命题正确.
,根据增函数的定义可知此命题正确.
⑤因为 的单调减区间是
的单调减区间是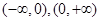 ,但
,但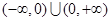 不是其单调递区间.错.
不是其单调递区间.错.
考点:考小题考查了幂函数的定义,函数的奇偶性和单调性.
点评:掌握常用函数的定义和性质是解决本小题的关键.要注意单调性的定义以及对常用函数的单调性的理解和掌握.

练习册系列答案
相关题目
 成立,则f(x)在R上是增函数;
成立,则f(x)在R上是增函数; 的单调减区间是(-∞,0)∪(0,+∞).
的单调减区间是(-∞,0)∪(0,+∞).