摘要:证明过程或演算步骤) 15-16.(本题是选做题.满分28分.请在下面四个题目中选两个作答.每小题14分.多做按前两题给分) A. 如图.△ABC是⊙O的内接三角形.PA是⊙O的切线.PB交AC于点E.交⊙O于点D.若PE=PA..PD=1.BD=8.求线段BC的长. B. 在直角坐标系中.已知椭圆.矩阵阵..求在矩阵作用下变换所得到的图形的面积. C.(选修4-4:坐标系与参数方程) 直线(为参数.为常数且)被以原点为极点.轴的正半轴为极轴.方程为的曲线所截.求截得的弦长. D. 设.求证:.17. 已知为直线.及所围成的面积.为直线.及所围成图形的面积(为常数). (1)若时.求, (2)若.求的最大值.
网址:http://m.1010jiajiao.com/timu_id_4456778[举报]
必做题:解答时应写出文字说明、证明过程或演算步骤.
已知函数f(x)=ln(ax+1)+
,x≥0,其中a>0.
(1)若f(x)在x=1处取得极值,求a的值;
(2)若f(x)的最小值为1,求a的取值范围.
查看习题详情和答案>>
已知函数f(x)=ln(ax+1)+
| 1-x | 1+x |
(1)若f(x)在x=1处取得极值,求a的值;
(2)若f(x)的最小值为1,求a的取值范围.
【选做题】在A,B,C,D四小题中只能选做2题,每题10分,共计20分.请在答题卡指定区域内作答,解答时写出文字说明、证明过程或演算步骤.
21-1.(选修4-2:矩阵与变换)
设M是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸压变换.
(1)求矩阵M的特征值及相应的特征向量;
(2)求逆矩阵M-1以及椭圆
+
=1在M-1的作用下的新曲线的方程.
21-2.(选修4-4:参数方程)
以直角坐标系的原点O为极点,x轴的正半轴为极轴.已知点P的直角坐标为(1,-5),点M的极坐标为(4,
),若直线l过点P,且倾斜角为
,圆C以M为圆心、4为半径.
(1)求直线l关于t的参数方程和圆C的极坐标方程;
(2)试判定直线l和圆C的位置关系.
查看习题详情和答案>>
21-1.(选修4-2:矩阵与变换)
设M是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸压变换.
(1)求矩阵M的特征值及相应的特征向量;
(2)求逆矩阵M-1以及椭圆
| x2 |
| 4 |
| y2 |
| 9 |
21-2.(选修4-4:参数方程)
以直角坐标系的原点O为极点,x轴的正半轴为极轴.已知点P的直角坐标为(1,-5),点M的极坐标为(4,
| π |
| 2 |
| π |
| 3 |
(1)求直线l关于t的参数方程和圆C的极坐标方程;
(2)试判定直线l和圆C的位置关系.
 (选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
(选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.A.选修4-1:几何证明选讲
如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过
N点的切线交CA的延长线于P.
(1)求证:PM2=PA•PC;
(2)若⊙O的半径为2
| 3 |
| 3 |
B.选修4-2:矩阵与变换
曲线x2+4xy+2y2=1在二阶矩阵M=
|
C.选修4-4:坐标系与参数方程
在极坐标系中,圆C的极坐标方程为ρ=
| 2 |
| π |
| 4 |
|
D.选修4-5:不等式选讲
设a,b,c均为正实数.
(1)若a+b+c=1,求a2+b2+c2的最小值;
(2)求证:
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
 选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.A.选修4-1:几何证明选讲
如图,PA切⊙O于点A,D为PA的中点,过点D引割线交⊙O于B、C两点.求证:∠DPB=∠DCP.
B.选修4-2:矩阵与变换
设M=
|
|
C.选修4-4:坐标系与参数方程
在极坐标系中,圆C的极坐标方程为ρ=
| 2 |
| π |
| 4 |
|
D.选修4-5:不等式选讲
解不等式:|2x+1|-|x-4|<2.
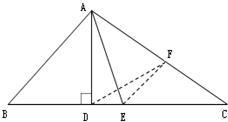 (几何证明选讲)解答时应写出文字说明、证明过程或演算步骤.△ABC中,AB<AC,AD、AE分别是BC边上的高和中线,且∠BAD=∠EAC.证明∠BAC是直角.
(几何证明选讲)解答时应写出文字说明、证明过程或演算步骤.△ABC中,AB<AC,AD、AE分别是BC边上的高和中线,且∠BAD=∠EAC.证明∠BAC是直角.