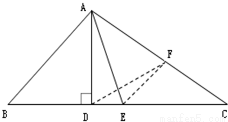
题目内容
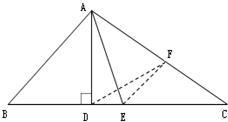 (几何证明选讲)解答时应写出文字说明、证明过程或演算步骤.△ABC中,AB<AC,AD、AE分别是BC边上的高和中线,且∠BAD=∠EAC.证明∠BAC是直角.
(几何证明选讲)解答时应写出文字说明、证明过程或演算步骤.△ABC中,AB<AC,AD、AE分别是BC边上的高和中线,且∠BAD=∠EAC.证明∠BAC是直角.分析:取AC中点F,连EF、DF,由三角形的中位线定理,易得EF∥AB,结合∠BAD=∠EAC易得∠EAB=∠DAC,∠ADF=∠DAC,进而得到A、D、E、F四点共圆,由圆内接四边形的性质得到EF⊥AC,进而AB⊥AC,即得到结论.
解答: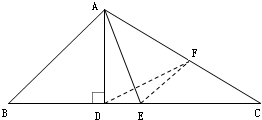 证明:如图,取AC中点F,连EF、DF,EF为三角形△ABC得中位线,故有EF∥AB,∠AEF=∠EAB.①
证明:如图,取AC中点F,连EF、DF,EF为三角形△ABC得中位线,故有EF∥AB,∠AEF=∠EAB.①
又由∠BAD=∠EAC,所以∠EAB=∠DAC.②
因AD是BC边上的高,则△ADC是直角三角形,则DF=AF.于是∠ADF=∠DAC.…③
联合①、②,得∠ADF=∠AEF,由此,得A、D、E、F四点共圆.
于是,∠AFE=180°-∠ADE=90°.因∠BAC+∠AFE=180°,故∠BAC=90°
最后一步,也可由:AD⊥BC得EF⊥ACC从而AB⊥AC,得∠BAC=90°.
又取AC的中点F,连EF,也可证得∠BAC=90°.
 证明:如图,取AC中点F,连EF、DF,EF为三角形△ABC得中位线,故有EF∥AB,∠AEF=∠EAB.①
证明:如图,取AC中点F,连EF、DF,EF为三角形△ABC得中位线,故有EF∥AB,∠AEF=∠EAB.①又由∠BAD=∠EAC,所以∠EAB=∠DAC.②
因AD是BC边上的高,则△ADC是直角三角形,则DF=AF.于是∠ADF=∠DAC.…③
联合①、②,得∠ADF=∠AEF,由此,得A、D、E、F四点共圆.
于是,∠AFE=180°-∠ADE=90°.因∠BAC+∠AFE=180°,故∠BAC=90°
最后一步,也可由:AD⊥BC得EF⊥ACC从而AB⊥AC,得∠BAC=90°.
又取AC的中点F,连EF,也可证得∠BAC=90°.
点评:本题考查的知识点是四点共圆的判定与性质,其中添加适当的辅助线,并根据已知条件得到A、D、E、F四点共圆,是解答本题的关键.

练习册系列答案
相关题目
 附加题 选做题在A、B、C、D四小题中只能选做两小题,每小题10分,共计20分,解答时应写出文字说明、证明过程或演算步骤.
附加题 选做题在A、B、C、D四小题中只能选做两小题,每小题10分,共计20分,解答时应写出文字说明、证明过程或演算步骤. 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.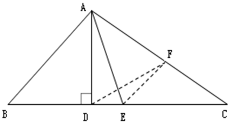 (几何证明选讲)解答时应写出文字说明、证明过程或演算步骤.△ABC中,AB<AC,AD、AE分别是BC边上的高和中线,且∠BAD=∠EAC.证明∠BAC是直角.
(几何证明选讲)解答时应写出文字说明、证明过程或演算步骤.△ABC中,AB<AC,AD、AE分别是BC边上的高和中线,且∠BAD=∠EAC.证明∠BAC是直角.