摘要:例1 设A.B是轴上的两点.点P的横坐标为2.且|PA|=|PB|.若直线PA的方程为.则直线PB的方程是 A. B. 2 C. D. 解法一:由得A. 又|PA|=|PB|知点P为AB中垂线上的点.故B(5.0).且所求直线的倾斜角与已知直线倾斜角互补.则斜率互为相反数.故所求直线的斜率为-1.所以选C. 解法二:=0代入得A. 由解得P(2.3). 设B(,0).由|PA|=|PB|解得=5. 由两点式 整理得PB直线方程:.故选C 例2 已知过原点O的一条直线与函数的图像交于A.B两点.分别过点A.B作轴的平行线与函数的的图像交于C.D两点. (Ⅰ)证明点C.D和原点O在同一条直线上, (Ⅱ)当BC平行于轴时.求点A的坐标. 解:(Ⅰ)设点A.B的横坐标分别为.由题设知.>1.>1.则点A.B纵坐标分别为.. 因为A.B在过点O的直线上.所以. 点C.D坐标分别为(.).(.). 由于=-3.==3 OC的斜率 . OD的斜率 . 由此可知..即O.C.D在同一条直线上. (Ⅱ)由于BC平行于x轴知= . 即得 =.∴ . 代入= 得=3. 由于>1知≠0.∴ =3. 考虑>1解得=.于是点A的坐标为(. )
网址:http://m.1010jiajiao.com/timu_id_4454177[举报]
假设银行1年定期的年利率为2%.某人为观看2008年的奥运会,从2001年元旦开始在银行存款1万元,存期1年,第二年元旦再把1万元和前一年的存款本利和一起作为本金再存1年定期存款,以后每年元旦都这样存款,则到2007年年底,这个人的银行存款共有(精确到0.01万元)( )
查看习题详情和答案>>
6、我国储蓄存款采取实名制并征收利息税,利息税由各银行储蓄点代扣代收.某人在2001年9月存入人民币1万元,存期一年,年利率为2.25%,到期时净得本金和利息共计10180元,则利息税的税率是( )
查看习题详情和答案>>
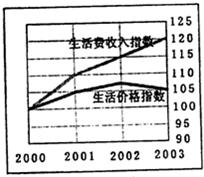 8、如图是一份从2000年初到2003年初的统计图表,根据此图表得到以下说法中,正确的有( )
8、如图是一份从2000年初到2003年初的统计图表,根据此图表得到以下说法中,正确的有( )