题目内容
从1998年到2001年期间,甲每年5月1日都到银行存入m元的一年定期储蓄,若年利率为t保持不变且计复利,到2002年5月1日,甲仅去取款,则可取回本息共( )元.
分析:本题以实际背景为依托属于数列应用题,在解答的过程当中,要特别注意逐年的进行列举,间隔比较大的要充分利用其规律找到结束的临界项,间隔较小的可以利用其规律直接解出即可.此题就属于后者.
解答:解:由题意知:
1998年5月1日存入金额为:m,
1999年5月1日存入金额为:m(1+t)+m,
2000年5月1日存入金额为:m(1+t)2+m(1+t)+m
2001年5月1日存入金额为:m(1+t)3+m(1+t)2+m(1+t)+m
2002年5月1日取回的金额为:
m(1+t)4+m(1+t)3+m(1+t)2+m(1+t)
=m•
=
[(1+t)5-(1+t)]元.
故选D.
1998年5月1日存入金额为:m,
1999年5月1日存入金额为:m(1+t)+m,
2000年5月1日存入金额为:m(1+t)2+m(1+t)+m
2001年5月1日存入金额为:m(1+t)3+m(1+t)2+m(1+t)+m
2002年5月1日取回的金额为:
m(1+t)4+m(1+t)3+m(1+t)2+m(1+t)
=m•
| (1+t)[1-(1+t)4] |
| 1-1-t |
=
| m |
| t |
故选D.
点评:本题属于数列应用题,按照规律列举是解决此类问题的一个重要方法.在此题中着重考查了增长率在数列当中的应用,同时考查了等比数列求和的知识.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
我国从1998年到2002年,每年的国内生产总值如下表:
| 年份 | 1998 | 1999 | 2000 | 2001 | 2002 |
| 生产总值(亿元) | 78345 | 82067 | 89442 | 95933 | 102398 |
(Ⅰ)根据已知数据,估计我国2003年的国内生产总值;
(Ⅱ)据资料可知我国2003年的国内生产总值为116694亿元,你的预测是否准确,若误差较大,能修正你所构造的模型吗?
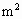 ,当地主管部门决定今后四年内仍按这个比例发展下去,则从2002年到2005年种植的绿色植被为(四舍五入)
,当地主管部门决定今后四年内仍按这个比例发展下去,则从2002年到2005年种植的绿色植被为(四舍五入) [(1+t)4-(1+t)]
[(1+t)4-(1+t)]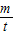 [(1+t)4-(1+t)]
[(1+t)4-(1+t)]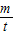 [(1+t)5-(1+t)]
[(1+t)5-(1+t)]