摘要: 甲.乙二人进行一次围棋比赛.约定先胜三局者获得这次比赛胜利.比赛结束.假设在一局中.甲获胜的概率为0.6.乙获胜的概率为0.4.各局比赛相互独立.已知前2局中甲乙各胜一局. (1)求再赛2局结束这次比赛的概率; (2)甲获得这次比赛胜利的概率.
网址:http://m.1010jiajiao.com/timu_id_4445684[举报]
(本小题满分12分)
甲、乙、丙三人进行象棋比赛,每两人比赛一场,共赛三场.每场比赛胜者得3分,负者得0分,没有平局,在每一场比赛中,甲胜乙的概率为![]() ,甲胜丙的概率为
,甲胜丙的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() 。
。
(1)求甲获第一名且丙获第二名的概率:
(2)设在该次比赛中,甲得分为ξ,求ξ的分布列和数学期望。
查看习题详情和答案>>本小题满分12分)
象棋比赛中,胜一局得2分,负一局得0分,和棋一局得1分,在甲对乙的每局比赛中,甲胜、负、和的概率依次为0.5,0.3,0.2.现此二人进行两局比赛,得分累加。
(I)求甲得2分的概率;
(II)记甲得分为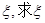 的分布列和期望。
的分布列和期望。
查看习题详情和答案>>
(本小题满分12分)
某校选拔若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为 ,
,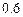 ,
,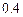 。第二次选拔,甲、乙、丙三人合格的概率依次为
。第二次选拔,甲、乙、丙三人合格的概率依次为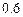 ,
, ,
, 。
。
(1)求第一次选拔后甲、乙两人中只有甲合格的概率;
(2)分别求出甲、乙、丙三人经过前后两次选拔后合格的概率;
(3)设甲、乙、丙经过前后两次选拔后恰有两人合格的的概率;
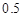 ,
, ,
, 。第二次选拔,甲、乙、丙三人合格的概率依次为
。第二次选拔,甲、乙、丙三人合格的概率依次为 满分12分)在某次足球比赛中,甲
满分12分)在某次足球比赛中,甲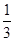 ,甲胜丙的概率为
,甲胜丙的概率为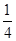 ,乙
,乙 胜丙的概率为
胜丙的概率为