摘要：3．如图2-4-48.在△ABC中.∠B=900.点P从点A开始沿AB边向点B以1㎝/秒的速度移动.点Q从点B开始沿BC边向点C以2㎝/秒的速度移动．(1)如果P.Q分别从A.B同时出发.几秒后△PBQ的面积等于8㎝2?(2)如果P.Q分别从A.B同时出发.点P到达点B后又继续沿BC边向点C移动.点Q到达点C后又继续沿CA边向点A移动.在这一整个移动过程中.是否存在点P.Q.使△PBQ的面积等于9㎝2?若存在.试确定P.Q的位置,若不存在.请说明理由．
网址：http://m.1010jiajiao.com/timu_id_4443137[举报]
如图：一艘轮船在上午8时从A处出发，以20海里/时的速度由南向北航行，在A处测得小岛P在北偏西24°，9点30分到达B处，这时测得小岛P在北偏西48°，求B处到小岛P的距离．
21、根据“十一五”规划，元双（双柏-元谋）高速工路即将动工．工程需要测量某一条河的宽度．如图，一测量员在河岸边的A处测得对岸岸边的一根标杆B在它的正北方向，测量员从A点开始沿岸边向正东方向前进100米到达点C处，测得∠ACB=68度．求所测之处河AB的宽度．（sin68°≈0.93，cos68°≈0.37，tan68°≈2.48）
数形结合作为一种数学思想方法，数形结合的应用大致又可分为两种情形：或者借助于数的精确性来阐明形的某些属性，即“以数解形”；或者借助形的几何直观性来阐明数之间的某种关系，即“以形助数”．
如浙教版九上课本第109页作业题第2题：如图1，已知在△ABC中，∠ACB=90°，CD⊥AB，D为垂足．易证得两个结论：（1）AC•BC=AB•CD （2）AC2=AD•AB
（1）请你用数形结合的“以数解形”思想来解：如图2，已知在△ABC中（AC＞BC），∠ACB=90°，CD⊥AB，D为垂足，CM平分∠ACB，且BC、AC是方程x2-14x+48=0的两个根，求AD、MD的长．
（2）请你用数形结合的“以形助数”思想来解：设a、b、c、d都是正数，满足a：b=c：d，且a最大．求证：a+d＞b+c（提示：不访设AB=a，CD=d，AC=b，BC=c，构造图1）
查看习题详情和答案>>
如浙教版九上课本第109页作业题第2题：如图1，已知在△ABC中，∠ACB=90°，CD⊥AB，D为垂足．易证得两个结论：（1）AC•BC=AB•CD （2）AC2=AD•AB
（1）请你用数形结合的“以数解形”思想来解：如图2，已知在△ABC中（AC＞BC），∠ACB=90°，CD⊥AB，D为垂足，CM平分∠ACB，且BC、AC是方程x2-14x+48=0的两个根，求AD、MD的长．
（2）请你用数形结合的“以形助数”思想来解：设a、b、c、d都是正数，满足a：b=c：d，且a最大．求证：a+d＞b+c（提示：不访设AB=a，CD=d，AC=b，BC=c，构造图1）
查看习题详情和答案>>
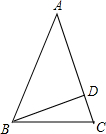如图：已知：在△ABC中，AB=AC，BD⊥AC于D，若∠DBC=24°，则∠A=