题目内容
如图：一艘轮船在上午8时从A处出发，以20海里/时的速度由南向北航行，在A处测得小岛P在北偏西24°，9点30分到达B处，这时测得小岛P在北偏西48°，求B处到小岛P的距离．分析：先根据平角的定义求出∠PBA的度数，由三角形内角和定理得出∠A=∠P，故可得出PB=AB即可．
解答：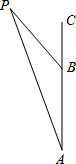
解：∵∠PBC=48°，
∴∠PBA=180°-48°=132°，
∵∠A=24°，
∴∠P=180°-132°-24°=24°，
∴∠A=∠P，
∴PB=AB，
∵轮船在上午8时从A处出发，以20海里/时的速度由南向北航行，9点30分到达B处，
∴AB=20×1.5=30（海里）．
答：B处到小岛P的距离为30海里．
解：∵∠PBC=48°，∴∠PBA=180°-48°=132°，
∵∠A=24°，
∴∠P=180°-132°-24°=24°，
∴∠A=∠P，
∴PB=AB，
∵轮船在上午8时从A处出发，以20海里/时的速度由南向北航行，9点30分到达B处，
∴AB=20×1.5=30（海里）．
答：B处到小岛P的距离为30海里．
点评：本题考查的是等腰三角形的判定与性质，解答此类题目时往往用到三角形的内角和等于180°这一隐含条件．
练习册系列答案
相关题目
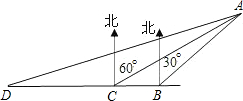时到达C处，这时测得小岛A在北偏东60°方向．如果轮船仍继续向正西方向航行，于上午11时到达D处，这时轮船与小岛A相距多远？
如图，一艘轮船在40海里/时的速度由西向东航行，上午8时到达A处，测得灯塔P在北偏东60°方向上；10时到达B处，测得灯塔P在北偏东30°方向上．当轮船到达灯塔P的正南时，轮船距灯塔P多远？
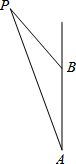如图：一艘轮船在上午8时从A处出发，以20海里/时的速度由南向北航行，在A处测得小岛P在北偏西24°，9点30分到达B处，这时测得小岛P在北偏西48°，求B处到小岛P的距离．
分到达B处,这时测得小岛P在北偏西48°，求B处到小岛P的距离.