题目内容
数形结合作为一种数学思想方法,数形结合的应用大致又可分为两种情形:或者借助于数的精确性来阐明形的某些属性,即“以数解形”;或者借助形的几何直观性来阐明数之间的某种关系,即“以形助数”.如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=90°,CD⊥AB,D为垂足.易证得两个结论:(1)AC•BC=AB•CD (2)AC2=AD•AB
(1)请你用数形结合的“以数解形”思想来解:如图2,已知在△ABC中(AC>BC),∠ACB=90°,CD⊥AB,D为垂足,CM平分∠ACB,且BC、AC是方程x2-14x+48=0的两个根,求AD、MD的长.
(2)请你用数形结合的“以形助数”思想来解:设a、b、c、d都是正数,满足a:b=c:d,且a最大.求证:a+d>b+c(提示:不访设AB=a,CD=d,AC=b,BC=c,构造图1)

分析:(1)首先通过解方程x2-14x+48=0求得AC、AB的值(AC>AB)(观察图形得知),根据勾股定理求得AB=10;然后由△ACD∽△ABC的性质求得AD=6.4;最后由角平分线的性质求得MD的值;
(2)设AB=a,CD=d,AC=b,BC=c,构造图1,由S△ABC=
底×高求得AB•CD=AC•BC,所以2AB•CD=2AC•BC①;再由勾股定理,得AB2=AC2+BC2②,根据①②解得(AB+CD)2>(AC+BC)2,即a+d>b+c.
(2)设AB=a,CD=d,AC=b,BC=c,构造图1,由S△ABC=
| 1 |
| 2 |
解答: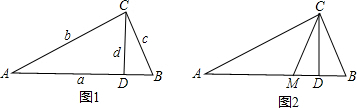 解:(1)显然,方程x2-14x+48=0的两根为6和8,
解:(1)显然,方程x2-14x+48=0的两根为6和8,
又AC>BC,
∴AC=8,BC=6,
由勾股定理AB=10;
△ACD∽△ABC,得AC2=AD•AB,
∴AD=6.4;
∵CM平分∠ACB,
∴AM:MB=AC:CB,
解得,AM=
,
∴MD=AD-AM=
;
(2)解:不访设AB=a,CD=d,AC=b,BC=c.
由三角形面积公式,得AB•CD=AC•BC,
2AB•CD=2AC•BC;
又勾股定理,得AB2=AC2+BC2,
∴AB2+2AB•CD=AC2+BC2+2AC•BC(等式性质),
∴AB2+2AB•CD=(AC+BC)2,
∴AB2+2AB•CD+CD2>(AC+BC)2,
∴(AB+CD)2>(AC+BC)2;
又AB、CD、AC、BC均大于零,
∴AB+CD>AC+BC即a+d>b+c.
 解:(1)显然,方程x2-14x+48=0的两根为6和8,
解:(1)显然,方程x2-14x+48=0的两根为6和8,又AC>BC,
∴AC=8,BC=6,
由勾股定理AB=10;
△ACD∽△ABC,得AC2=AD•AB,
∴AD=6.4;
∵CM平分∠ACB,
∴AM:MB=AC:CB,
解得,AM=
| 40 |
| 7 |
∴MD=AD-AM=
| 24 |
| 35 |
(2)解:不访设AB=a,CD=d,AC=b,BC=c.
由三角形面积公式,得AB•CD=AC•BC,
2AB•CD=2AC•BC;
又勾股定理,得AB2=AC2+BC2,
∴AB2+2AB•CD=AC2+BC2+2AC•BC(等式性质),
∴AB2+2AB•CD=(AC+BC)2,
∴AB2+2AB•CD+CD2>(AC+BC)2,
∴(AB+CD)2>(AC+BC)2;
又AB、CD、AC、BC均大于零,
∴AB+CD>AC+BC即a+d>b+c.
点评:本题考查了相似三角形的判定与性质、勾股定理及因式分解法解一元二次方程.解答(2)的难点是由等式AB2+2AB•CD=AC2+BC2+2AC•BC(等式性质),推到出不等式(AB+CD)2>(AC+BC)2.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB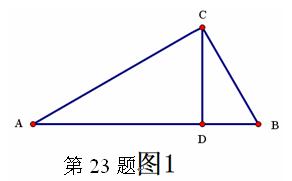
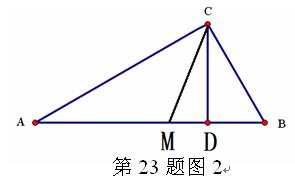
 几何直观性来阐明数之间的某种关系,即“以形助数”。 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
几何直观性来阐明数之间的某种关系,即“以形助数”。 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB

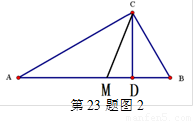 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB