摘要： (1)因为BE∥AC.AB∥CD. 所以四边形ABEC是平行四边形. 所以CE=AB=4. 所以△AED的面积为×4×＝16, (2)四边形APCD的面积与正方形ABCD的面积相等. 因为BE∥AC.所以△APC的面积与△ABC的面积相等. 所以△APC的面积+△ACD的面积＝△ABC的面积+△ACD的面积＝正方形ABCD的面积,
网址：http://m.1010jiajiao.com/timu_id_4435316[举报]
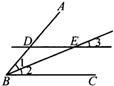16、请把下列证明过程补充完整：已知：如图，DE∥BC，BE平分∠ABC．求证：∠1=∠3．
证明：因为BE平分∠ABC（已知），
所以∠1=
∠2
（角平分线性质）．又因为DE∥BC（已知），
所以∠2=
∠3
（两直线平行，同位角相等）．所以∠1=∠3（角平分线性质）．
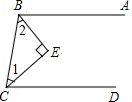有这样一道题：如图所示，已知BA∥CD，BE平分∠ABC，CE平分∠BCD，试判断∠1与∠2的度数有怎样的关系，并说明理由．小丽的判断是∠1与∠2互余，这是正确的，但是她写的说明不完整，请你给予补充．
因为BE是∠ABC的平分线，所以∠2=
| 1 |
| 2 |
∠ABC
∠ABC
．又因为CE是∠BCD的平分线，所以∠1=| 1 |
| 2 |
∠BCD
∠BCD
，于是∠1+∠2=| 1 |
| 2 |
∠ABC
∠ABC
+∠BCD
∠BCD
）．而AB∥CD，根据两直线平行，同旁内角互补，得
∠ABC
∠ABC
+∠BCD
∠BCD
=180°
180°
，所以∠1+∠2=90°，即∠1与∠2互余．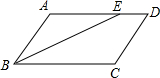
如图，已知BE平分∠ABC，E点在线段AD上，∠ABE=∠AEB，AD与BC平行吗？为什么？解：因为BE平分∠ABC
已知
已知
所以∠ABE=∠EBC
角平分线意义
角平分线意义
因为∠ABE=∠AEB
已知
已知
所以∠AEB=∠EBC
等量代换
等量代换
所以AD∥BC
内错角相等，两直线平行
内错角相等，两直线平行
．
已知，如图，BE平分∠ABC，DE∥BC，∠3=35°，求∠1的度数
请把下列证明过程补充完整．