摘要:2.已知 求证: 证明:由换底公式 由等比定理得: ∴ ∴
网址:http://m.1010jiajiao.com/timu_id_4421371[举报]
(文科)已知n2(n≥4且n∈N*)个正数排成一个n行n列的数阵:
第1列 第2列 第3列 …第n列
第1行 a1,1 a1,2 a1,3 …a1,n
第2行 a2,1 a2,2 a2,3 …a2,n
第3行 a3,1 a3,2 a3,3 …a3,n
…
第n行 an,1 an,2 an,3 …an,n
其中ai,k(i,k∈N*,且1≤i≤n,1≤k≤n)表示该数阵中位于第i行第k列的数,已知该数阵中各行的数依次成等比数列,各列的数依次成公比为2的等比数列,已知a2,3=8,a3,4=20.
(1)求a1,1a2,2;
(2)设An=a1,n+a2,n-1+a3,n-2+…+an,1求证:An+n能被3整除.
查看习题详情和答案>>
如图,已知P为矩形ABCD所在平面外一点,PA⊥平面ABCD,E、F分别是AB、PC的中点,
(Ⅰ)求证:EF∥平面PAD;
(Ⅱ)求证:EF⊥CD;
(Ⅲ)若∠PDA=45°,求EF与平面ABCD所成的角的大小。
(Ⅰ)求证:EF∥平面PAD;
(Ⅱ)求证:EF⊥CD;
(Ⅲ)若∠PDA=45°,求EF与平面ABCD所成的角的大小。

完成下列反证法证题的全过程:
已知0<a≤3,函数f(x)=x3-ax在区间[1,+∞)上是增函数,设当x0≥1,f(x0)≥1时,有f(f(x0))=x0,求证:f(x0)=x0.
证明:假设f(x0)≠x0,则必有 ① 或 ② .
若 ③ ,由f(x)在区间[1,+∞)上是增函数,则f(f(x0))>f(x0).
又f(f(x0))=x0,所以f(x0)<x0,这与 ④ 矛盾.
若x0>f(x0)≥1,由f(x)在区间[1,+∞)上是增函数,则 ⑤ .
又f(f(x0))=x0,所以f(x0)>x0,这与 ⑥ 矛盾.
综上所述,当x0≥1,f(x0)≥1且f(f(x0))=x0时,有f(x0)=x0.
 中,
中, ,
,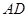 斜边
斜边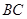 上的高,以
上的高,以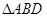 折
起,使
折
起,使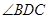 为直角。
为直角。 平面
平面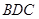 ;(2)求证:
;(2)求证: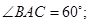
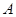 到平面
到平面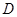 到平面
到平面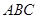 的距离;
的距离;