摘要:解析:(1)机械能守恒定律得. ① 根据牛顿第二定律得. ② 联立以上两式代入数据得FN=3.0×103N ③ (2)若滑上木板A时.木板不动. ④ 若滑上木板B时.木板B开始滑动.由受力分析得 ⑤ 联立④⑤式代入数据得 ⑥ (3)① .由⑥式知.货物在木板A上滑动时.木板不动.货物滑上B.B滑动.货物在木板A上做减速运动时的加速度大小为. ⑦ 设货物滑到木板A末端是的速度为.由运动学公式得 ⑧ 联立①⑦⑧式代入数据得v=4.0 m/s ⑨ ②货物在B上.它向右做匀减速运动.对B: m 22=u1m1g-u2(m1+m2)g 2=1m/s2 ⑩ 假设二者能共速:v共=v1-1t2 ⑾ v共=2t2 ⑿ 在木板B上运动的时间: t2=0.67s ⒀ s2=v12-v共2/21 ⒁ SB=v共2/22 ⒂ 物相对于B运动的位移:s相=s2- SB =4/3m<2m ∴假设成立 ⒃ ① ② 式各2分.其余各式各1分
网址:http://m.1010jiajiao.com/timu_id_4418510[举报]
已知函数 的最小值为0,其中
的最小值为0,其中
(Ⅰ)求 的值;
的值;
(Ⅱ)若对任意的 有
有 ≤
≤ 成立,求实数
成立,求实数 的最小值;
的最小值;
(Ⅲ)证明 (
( ).
).
【解析】(1)解:
 的定义域为
的定义域为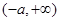

由 ,得
,得
当x变化时, ,
, 的变化情况如下表:
的变化情况如下表:
|
x |
|
|
|
|
|
- |
0 |
+ |
|
|
|
极小值 |
|
因此, 在
在 处取得最小值,故由题意
处取得最小值,故由题意 ,所以
,所以
(2)解:当 时,取
时,取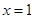 ,有
,有 ,故
,故 时不合题意.当
时不合题意.当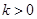 时,令
时,令 ,即
,即

令 ,得
,得
①当 时,
时, ,
, 在
在 上恒成立。因此
上恒成立。因此 在
在 上单调递减.从而对于任意的
上单调递减.从而对于任意的 ,总有
,总有 ,即
,即 在
在 上恒成立,故
上恒成立,故 符合题意.
符合题意.
②当 时,
时, ,对于
,对于 ,
, ,故
,故 在
在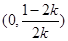 上单调递增.因此当取
上单调递增.因此当取 时,
时, ,即
,即 不成立.
不成立.
故 不合题意.
不合题意.
综上,k的最小值为 .
.
(3)证明:当n=1时,不等式左边= =右边,所以不等式成立.
=右边,所以不等式成立.
当 时,
时,


在(2)中取 ,得
,得
 ,
,
从而

所以有





综上,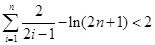 ,
,
查看习题详情和答案>>

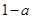


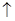
 的各项均为正数.若对任意的
的各项均为正数.若对任意的 ,存在
,存在 ,使得
,使得 成立,则称数列
成立,则称数列 ,
, ,求
,求 ;
; ,
, ,
, ,
, ,…成等比数列,且公比
,…成等比数列,且公比 ,
,
 }是“j4型”数列,得
}是“j4型”数列,得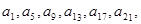 ,…成等比数列,设公比为t. 由{
,…成等比数列,设公比为t. 由{ ,…成等比数列,设公比为
,…成等比数列,设公比为 ;
; ,…成等比数列,设公比为
,…成等比数列,设公比为 ;
; …成等比数列,设公比为
…成等比数列,设公比为 ;
; 关于行驶速度
关于行驶速度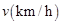 的函数解析式可以表示为:
的函数解析式可以表示为: .已知甲、乙两地相距
.已知甲、乙两地相距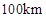 ,设汽车的行驶速度为
,设汽车的行驶速度为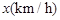 ,从甲地到乙地所需时间为
,从甲地到乙地所需时间为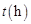 ,耗油量为
,耗油量为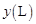 .
.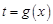 及
及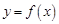 ;
;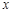 为多少时,
为多少时,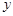 取得最小值,并求出这个最小值.
取得最小值,并求出这个最小值.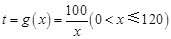 ,根据
,根据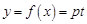 可求出y=f(x).
可求出y=f(x).