题目内容
求下列函数的解析式:(1)已知f(x)=x2+2x,求f(2x+1);
(2)已知f(![]() -1)=x+2
-1)=x+2![]() ,求f(x);
,求f(x);
(3)已知f(x)-![]() )=3x+2,求f(x).
)=3x+2,求f(x).
(1)解:f(2x+1)=(2x+1)2+2(2x+1)= 4x2+8x+3.
(2)解法一:拼凑法.
f(![]() -1)=(
-1)=(![]() -1)2+4(
-1)2+4(![]() -1)+3.
-1)+3.
而![]() -1≥-1.
-1≥-1.
故所求的函数f(x)=x2+4x+3(x≥-1).
解法二:换元法.
令t=![]() -1,则t≥-1,且
-1,则t≥-1,且![]() =t+1,
=t+1,
∴f(t)=(t+1)2+2(t+1)=t2+4t+3.
故所求的函数为f(x)=x2+4x+3(x≥-1).
(3)解:令t=![]() ,则x=
,则x=![]() ,∴f(
,∴f(![]() )-
)-![]() +2,
+2,
即f(![]() )-
)-![]() +2,与原式联立得
+2,与原式联立得
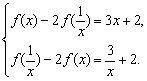
解得f(x)=-x-![]() -2.
-2.
故所求的函数为f(x)=-x-![]() -2.
-2.
点评:求函数解析式的常见方法:代入法、待定系数法、拼凑法、换元法、方程组法等.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目