摘要:20. 已知f(x)=x+lnx.x∈(0.e]..其中e=2.71828-是自然对数的底数.∈R. (1)若=-1.求f(x)的极值, 的条件下. , (3)是否存在实数.使f(x)的最大值是-3.如果存在.求出的值,如果不存在.说明理由. 中山市高二级2008-2009学年度第二学期期末统一考试
网址:http://m.1010jiajiao.com/timu_id_4410215[举报]
(本小题满分14分)
已知a∈R,函数 ,g(x)=(lnx-1)ex+x(其中e为自然对数的底数).(1)判断函数f(x)在
,g(x)=(lnx-1)ex+x(其中e为自然对数的底数).(1)判断函数f(x)在 上的单调性;(2)是否存在实数
上的单调性;(2)是否存在实数 ,使曲线y=g(x)在点x=x0处的切线与y轴垂直? 若存在,求出x0的值;若不存在,请说明理由.(3)若实数m,n满足m>0, n>0,求证:nnem≥mnen.
,使曲线y=g(x)在点x=x0处的切线与y轴垂直? 若存在,求出x0的值;若不存在,请说明理由.(3)若实数m,n满足m>0, n>0,求证:nnem≥mnen.
查看习题详情和答案>>
(本题满分14分)
已知函数f(x)=lnx+
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设m R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
(Ⅲ)证明:ln2 l+ 1n22,+…+ln2
n> ∈N*).
∈N*).
查看习题详情和答案>>
(本题满分14分)
已知函数f(x)=lnx+
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设m R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
(Ⅲ)证明:ln2 l+ 1n22,+…+ln2 n> ∈N*).
∈N*).
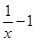
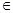 R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;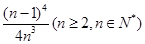 ∈N*).
∈N*).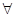 x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围; +1≤0恒成立,求实数a的取值范围.
+1≤0恒成立,求实数a的取值范围.