摘要：例1.求函数的最大值和最小值. 例2.在平面直角坐标系中有点.. (1)求向量的夹角的余弦值用表示的函数, (2)求的最值. 例3.如图.某海滨浴场的岸边可近似地看作直线.救生员现在岸边的A处.发现海中的B处有人求救.救生员没有直接从A处游向B处.而是沿岸边A跑到离B最近的D处.然后游向B处.若救生员在岸边的行进速度为6米/秒.在海水中的行进速度为2米/秒. (1)分析救生员的选择是否正确? (2)在AD上找一处C.使救生员从A到B的时间最短.并求出最短时间. 例4.已知函数. (1)证明:当时.经过图象上的任意两点的直线的斜率恒为负数, (2)设有不相等的实数..且.求+的值. 例5.已知向量. 求的值.
网址：http://m.1010jiajiao.com/timu_id_4409200[举报]
函数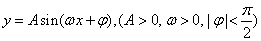
的最小值是
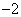，在一个周期内图象最高点与最低点横坐标差是
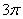，又：图象过点
，
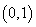求（1）函数解析式，
（2）函数的最大值、以及达到最大值时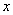
的集合；
（3）该函数图象可由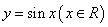
的图象经过怎样的平移和伸缩得到？
（4）当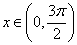
时，函数的值域.
查看习题详情和答案>>
函数
的最小值是
，在一个周期内图象最高点与最低点横坐标差是
，又：图象过点
，
求（1）函数解析式，
（2）函数的最大值、以及达到最大值时
的集合；
（3）该函数图象可由
的图象经过怎样的平移和伸缩得到？
（4）当
时，函数的值域.
函数
的最小值是
，在一个周期内图象最高点与最低点横坐标差是
，又：图象过点
，
求（1）函数解析式，
（2）函数的最大值、以及达到最大值时
的集合；
（3）该函数图象可由
的图象经过怎样的平移和伸缩得到？
（4）当
时，函数的值域.
的最小值是，在一个周期内图象最高点与最低点横坐标差是，又：图象过点，求（1）函数解析式，
（2）函数的最大值、以及达到最大值时
的集合；（3）该函数图象可由
的图象经过怎样的平移和伸缩得到？（4）当
时，函数的值域.
在平面直角坐标系中，已知O为坐标原点，点A的坐标为（a，b），点B的坐标为（cosωx，sinωx），其中a2+b2≠0且ω＞0．设f(x)=
•
．
（1）若a=
，b=1，ω=2，求方程f（x）=1在区间[0，2π]内的解集；
（2）若点A是过点（-1，1）且法向量为
=(-1，1)的直线l上的动点．当x∈R时，设函数f（x）的值域为集合M，不等式x2+mx＜0的解集为集合P．若P⊆M恒成立，求实数m的最大值；
（3）根据本题条件我们可以知道，函数f（x）的性质取决于变量a、b和ω的值．当x∈R时，试写出一个条件，使得函数f（x）满足“图象关于点(
，0)对称，且在x=
处f（x）取得最小值”．
查看习题详情和答案>>
| OA |
| OB |
（1）若a=
| 3 |
（2）若点A是过点（-1，1）且法向量为
| n |
（3）根据本题条件我们可以知道，函数f（x）的性质取决于变量a、b和ω的值．当x∈R时，试写出一个条件，使得函数f（x）满足“图象关于点(
| π |
| 3 |
| π |
| 6 |