题目内容
函数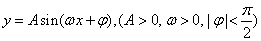 的最小值是
的最小值是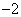 ,在一个周期内图象最高点与最低点横坐标差是
,在一个周期内图象最高点与最低点横坐标差是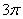 ,又:图象过点
,又:图象过点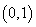 ,
,
求(1)函数解析式,
(2)函数的最大值、以及达到最大值时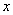 的集合;
的集合;
(3)该函数图象可由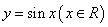 的图象经过怎样的平移和伸缩得到?
的图象经过怎样的平移和伸缩得到?
(4)当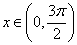 时,函数的值域.
时,函数的值域.
【答案】
(1)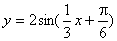 (2)2 (3)向左平移
(2)2 (3)向左平移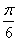 个单位,横坐标伸长到原来的3倍,纵坐标变为原来的2倍 (4)
个单位,横坐标伸长到原来的3倍,纵坐标变为原来的2倍 (4)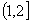
【解析】
试题分析:(1)易知:A =" 2" 半周期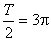 ∴T
= 6p 即
∴T
= 6p 即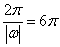 (
(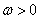 ) 从而:
) 从而: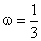 设:
设: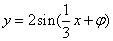 令x = 0 有
令x = 0 有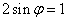 又:
又: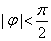 ∴
∴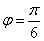
∴所求函数解析式为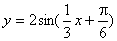 .
.
(2)令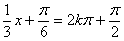 ,即
,即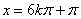 时,
时,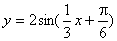 有最大值2,故当
有最大值2,故当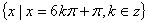 时,
时,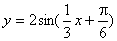 取最大值2 .
取最大值2 .
(3)因为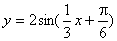 ,所以
,所以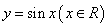 向左平移
向左平移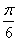 个单位得到
个单位得到 ,横坐标伸长到原来的3倍得到
,横坐标伸长到原来的3倍得到 ,纵坐标伸长到原来的2倍得到
,纵坐标伸长到原来的2倍得到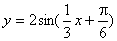 .
.
(4)因为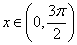 ,所以
,所以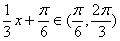 ,所以
,所以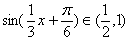 ,所以
,所以
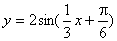
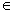
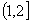 .
.
考点:由 的部分图象确定其解析式.
的部分图象确定其解析式.
点评:本题考查由 的部分图象确定其解析式,确定A,ω,φ的值是关键,φ的确定是难点,属于中档题.
的部分图象确定其解析式,确定A,ω,φ的值是关键,φ的确定是难点,属于中档题.

练习册系列答案
相关题目
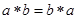 ;
;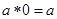 ; ③对任意
; ③对任意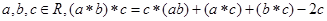
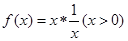 的最小值是
的最小值是