摘要：5．突出向量与其它数学知识的交汇 “新课程增加了新的现代数学内容.其意义不仅在于数学内容的更新.更重要的是引入新的思维方法.可以更有效地处理和解决数学问题和实际应用问题 .因此.新课程卷中有些问题属于新教材与旧教材的结合部.凡涉及此类问题.高考命题都采用了新旧结合.以新带旧或以新方法解决的方法进行处理.从中启示我们在高考学习中.应突出向量的工具性.注重向量与其它知识的交汇与融合.但不宜“深挖洞 .我们可以预测近两年向量高考题的难度不会也不应该上升到压轴题的水平.
网址：http://m.1010jiajiao.com/timu_id_4399503[举报]
选做题本题包括A，B，C，D四小题，请选定其中 两题 作答，每小题10分，共计20分，解答时应写出文字说明，证明过程或演算步骤．
A选修4-1：几何证明选讲
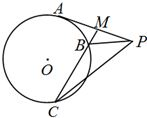
自圆O外一点P引圆的一条切线PA，切点为A，M为PA的中点，过点M引圆O的割线交该圆于B、C两点，且∠BMP=100°，∠BPC=40°，求∠MPB的大小．
B选修4-2：矩阵与变换
已知二阶矩阵A=
|
|
|
C选修4-4：坐标系与参数方程
在平面直角坐标系xOy中，已知曲线C的参数方程为
|
| π |
| 4 |
| 2 |
P为曲线C上的动点，求点P到直线l距离的最大值．
D选修4-5：不等式选讲
若正数a，b，c满足a+b+c=1，求
| 1 |
| 3a+2 |
| 1 |
| 3b+2 |
| 1 |
| 3c+2 |
本题包括高考A，B，C，D四个选题中的B，C两个小题，每小题10分，共20分．把答案写在答题卡相应的位置上．解答时应写出文字说明、证明过程或演算步骤．
B．选修4-2：矩阵与变换
已知矩阵A=
，向量
=
．求向量
，使得A2
=
．
C．选修4-4：极坐标与参数方程
在直角坐标系x0y中，直线l的参数方程为
（t为参数），若以直角坐标系xOy的O点为极点，Ox为极轴，且长度单位相同，建立极坐标系，得曲线C的极坐标方程为ρ=2cos(θ-
)．
（1）求直线l的倾斜角；
（2）若直线l与曲线l交于A、B两点，求AB．
查看习题详情和答案>>
B．选修4-2：矩阵与变换
已知矩阵A=
|
| β |
|
| α |
| α |
| β |
C．选修4-4：极坐标与参数方程
在直角坐标系x0y中，直线l的参数方程为
|
| π |
| 4 |
（1）求直线l的倾斜角；
（2）若直线l与曲线l交于A、B两点，求AB．
已知直线l的方向向量与向量
=（1，2）垂直，且直线l过点A（1，1），则直线l的方程为（ ）
| a |
| A、x-2y-1=0 |
| B、2x+y-3=0 |
| C、x+2y+1=0 |
| D、x+2y-3=0 |