摘要:类比上述方法.请你计算“ .其结果为
网址:http://m.1010jiajiao.com/timu_id_431368[举报]
在计算“1×2+2×3+…+n(n+1)”时,某同学学到了如下一种方法:先改写第k项:k(k+1)=
[k(k+1)(k+2)-(k-1)k(k+1)]由此得
1×2=
(1×2×3-0×1×2),
2×3=
(2×3×4-1×2×3)
…
n(n+1)=
[n(n+1)(n+2)-(n-1)n(n+1)]
相加,得1×2×3+…+n(n+1)=
n(n+1)(n+2)
类比上述方法,请你计算“1×2×3+2×3×4+…+n(n+1)(n+2)”,
其结果为 .
查看习题详情和答案>>
| 1 |
| 3 |
1×2=
| 1 |
| 3 |
2×3=
| 1 |
| 3 |
…
n(n+1)=
| 1 |
| 3 |
相加,得1×2×3+…+n(n+1)=
| 1 |
| 3 |
类比上述方法,请你计算“1×2×3+2×3×4+…+n(n+1)(n+2)”,
其结果为
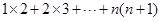 ”时,某同学学到了如下一种方法:先改写第k项:
”时,某同学学到了如下一种方法:先改写第k项: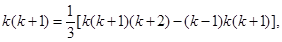 由此得
由此得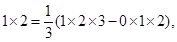
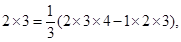
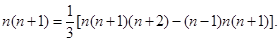
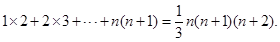
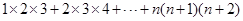 ”,
”, ”时,某同学学到了如下一种方法:先改写第
”时,某同学学到了如下一种方法:先改写第 项:
项: ,由此得
,由此得



 ”,其结果为
________.
”,其结果为
________.