摘要:又∵MH⊥AB, ∴MH∥AD ∴MH=AD
网址:http://m.1010jiajiao.com/timu_id_429725[举报]
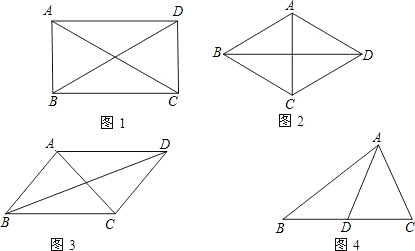
在探究矩形的性质时,小明得到了一个有趣的结论:矩形两条对角线的平方和等于四条边的平方和.如图1,在矩形ABCD中,由勾股定理,得AC2=AB2+BC2,BD2=AB2+AD2,又CD=AB,AD=BC,所以AC2+BD2=AB2+BC2+CD2+AD2=2(AB2+BC2).
小亮对菱形进行了探究,也得到了同样的结论,于是小亮猜想:任意平行四边形两条对角线的平方和等于四条边的平方和.请你解决下列问题:
(1)如图2,已知:四边形ABCD是菱形,求证:AC2+BD2=2(AB2+BC2);
(2)你认为小亮的猜想是否成立,如果成立,请利用图3给出证明;如果不成立,请举反例说明;
(3)如图4,在△ABC中,BC、AC、AB的长分别为a、b、c,AD是BC边上的中线.试求AD的长.(结果用a,b,c表示)
 查看习题详情和答案>>
查看习题详情和答案>>
小亮对菱形进行了探究,也得到了同样的结论,于是小亮猜想:任意平行四边形两条对角线的平方和等于四条边的平方和.请你解决下列问题:
(1)如图2,已知:四边形ABCD是菱形,求证:AC2+BD2=2(AB2+BC2);
(2)你认为小亮的猜想是否成立,如果成立,请利用图3给出证明;如果不成立,请举反例说明;
(3)如图4,在△ABC中,BC、AC、AB的长分别为a、b、c,AD是BC边上的中线.试求AD的长.(结果用a,b,c表示)
 查看习题详情和答案>>
查看习题详情和答案>>
在探究矩形的性质时,小明得到了一个有趣的结论:矩形两条对角线的平方和等于四条边的平方和.如图1,在矩形ABCD中,由勾股定理,得AC2=AB2+BC2,BD2=AB2+AD2,又CD=AB,AD=BC,所以AC2+BD2=AB2+BC2+CD2+AD2=2(AB2+BC2).
小亮对菱形进行了探究,也得到了同样的结论,于是小亮猜想:任意平行四边形两条对角线的平方和等于四条边的平方和.请你解决下列问题:
(1)如图2,已知:四边形ABCD是菱形,求证:AC2+BD2=2(AB2+BC2);
(2)你认为小亮的猜想是否成立,如果成立,请利用图3给出证明;如果不成立,请举反例说明;
(3)如图4,在△ABC中,BC、AC、AB的长分别为a、b、c,AD是BC边上的中线.试求AD的长.(结果用a,b,c表示)
查看习题详情和答案>>
在探究矩形的性质时,小明得到了一个有趣的结论:矩形两条对角线的平方和等于四条边的平方和.如图1,在矩形ABCD中,由勾股定理,得AC2=AB2+BC2,BD2=AB2+AD2,又CD=AB,AD=BC,所以AC2+BD2=AB2+BC2+CD2+AD2=2(AB2+BC2).
小亮对菱形进行了探究,也得到了同样的结论,于是小亮猜想:任意平行四边形两条对角线的平方和等于四条边的平方和.请你解决下列问题:
(1)如图2,已知:四边形ABCD是菱形,求证:AC2+BD2=2(AB2+BC2);
(2)你认为小亮的猜想是否成立,如果成立,请利用图3给出证明;如果不成立,请举反例说明;
(3)如图4,在△ABC中,BC、AC、AB的长分别为a、b、c,AD是BC边上的中线.试求AD的长.(结果用a,b,c表示)

查看习题详情和答案>>
小亮对菱形进行了探究,也得到了同样的结论,于是小亮猜想:任意平行四边形两条对角线的平方和等于四条边的平方和.请你解决下列问题:
(1)如图2,已知:四边形ABCD是菱形,求证:AC2+BD2=2(AB2+BC2);
(2)你认为小亮的猜想是否成立,如果成立,请利用图3给出证明;如果不成立,请举反例说明;
(3)如图4,在△ABC中,BC、AC、AB的长分别为a、b、c,AD是BC边上的中线.试求AD的长.(结果用a,b,c表示)

查看习题详情和答案>>
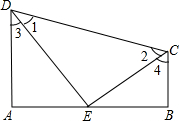 如图:已知DA⊥AB,DE平分∠ABC、CE平分∠BCD,且∠1+∠2=90°
如图:已知DA⊥AB,DE平分∠ABC、CE平分∠BCD,且∠1+∠2=90°求证:BC⊥AB.
证明:∵DE平分∠ADC、CE平分∠BCD(已知)
∵∠1=∠3,∠2=∠4(
又∵∠1+∠2=90°
∵∠1+∠2+∠3+∠4=180°
即:∠ADC+∠BCD=180°
∵AD∥BC (
∵∠A+∠B=180°(
又∵DA⊥AB ( 已知 )
∵∠A=90° (
∵∠B=90°
∵BC⊥AD (
21、解:因为∠B=∠C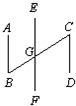
所以AB∥CD(
又因为AB∥EF
所以EF∥CD(
所以∠BGF=∠C(
(2)如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3
试说明:AD平分∠BAC
解:因为AD⊥BC,EG⊥BC
所以AD∥EG(
所以∠1=∠E(
∠2=∠3(
又因为∠3=∠E
所以∠1=∠2
所以AD平分∠BAC(
(3)如图,EF∥AD,∠1=∠2,∠BAC=70°.求∠AGD的度数.
解:因为EF∥AD,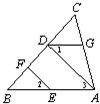
所以∠2=
又因为∠1=∠2
所以∠1=∠3 (
所以AB∥
所以∠BAC+
因为∠BAC=70°
所以∠AGD=
查看习题详情和答案>>

所以AB∥CD(
内错角相等,两直线平行
)又因为AB∥EF
所以EF∥CD(
平行线的传递性
)所以∠BGF=∠C(
两直线平行,同位角相等
)(2)如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3

试说明:AD平分∠BAC
解:因为AD⊥BC,EG⊥BC
所以AD∥EG(
同垂直于一条直线的两个垂线段平行
)所以∠1=∠E(
两直线平行,同位角相等
)∠2=∠3(
两直线平行,内错角相等
)又因为∠3=∠E
所以∠1=∠2
所以AD平分∠BAC(
等量代换
)(3)如图,EF∥AD,∠1=∠2,∠BAC=70°.求∠AGD的度数.
解:因为EF∥AD,

所以∠2=
3
(
两直线平行,同位角相等
)又因为∠1=∠2
所以∠1=∠3 (
等量代换
)所以AB∥
DG
(
内错角相等,两直线平行
)所以∠BAC+
∠DGA
=180°(
两直线平行,同旁内角互补
)因为∠BAC=70°
所以∠AGD=
110°