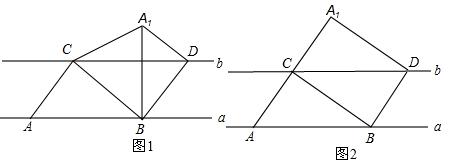
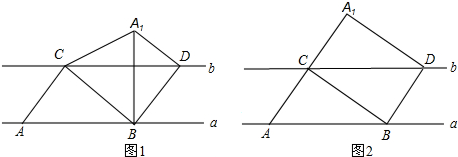题目内容
在探究矩形的性质时,小明得到了一个有趣的结论:矩形两条对角线的平方和等于四条边的平方和.如图1,在矩形ABCD中,由勾股定理,得AC2=AB2+BC2,BD2=AB2+AD2,又CD=AB,AD=BC,所以AC2+BD2=AB2+BC2+CD2+AD2=2(AB2+BC2).小亮对菱形进行了探究,也得到了同样的结论,于是小亮猜想:任意平行四边形两条对角线的平方和等于四条边的平方和.请你解决下列问题:
(1)如图2,已知:四边形ABCD是菱形,求证:AC2+BD2=2(AB2+BC2);
(2)你认为小亮的猜想是否成立,如果成立,请利用图3给出证明;如果不成立,请举反例说明;
(3)如图4,在△ABC中,BC、AC、AB的长分别为a、b、c,AD是BC边上的中线.试求AD的长.(结果用a,b,c表示)

【答案】分析:(1)设AC与BD相交于点O,根据四边形ABCD是菱形,得出AC=2OA,BD=2OB,利用勾股定理,得OA2+OB2=AB2,再利用AB=BC,即可求证AC2+BD2=2(AB2+BC2).
(2)作AE⊥BC于点E,DF⊥BC交BC的延长线于F,再根据四边形ABCD是平行四边形,求证△ABE≌△DCF,得出AE=DF,BE=CF,由勾股定理得AC2=AE2+EC2=AE2+(BC-BE)2,BD2=DF2+BF2=DF2+(BC+CF)2=AE2+(BC+BE)2
(3)延长AD到E,使DE=AD,连接BE,CE,则AE=2AD,求证四边形ABEC是平行四边形,由(2)的结论,得AE2+BC2=2(AB2+AC2),解得AD2=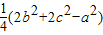 .
.
解答:解:(1)如图2,设AC与BD相交于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,AC=2OA,BD=2OB.
在Rt△AOB中,由勾股定理,得
OA2+OB2=AB2,
∴AC2+BD2=4OA2+4OB2=4(OA2+OB2)=4AB2,
又∵AB=BC,
∴AC2+BD2=2(AB2+AB2)=2(AB2+BC2).
(2)小亮的猜想成立.
证明:作AE⊥BC于点E,DF⊥BC交BC的延长线于F,
则∠AEB=∠DFC=90°.
∵四边形ABCD是平行四边形,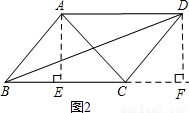
∴AB=DC,AB∥CD,
∴∠ABE=∠DCF,
∴△ABE≌△DCF,
∴AE=DF,BE=CF.
在Rt△ACE和Rt△BDF中,由勾股定理,得
AC2=AE2+EC2=AE2+(BC-BE)2,
BD2=DF2+BF2=DF2+(BC+CF)2=AE2+(BC+BE)2,
∴AC2+BD2=2AE2+2BC2+2BE2=2(AE2+BE2)+2BC2.
又AE2+BE2=AB2,
故AC2+BD2=2(AB2+BC2).
(3)延长AD到E,使DE=AD,连接BE,CE,则AE=2AD.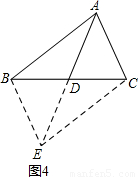
∵BD=CD,
∴四边形ABEC是平行四边形.
由(2)的结论,得
AE2+BC2=2(AB2+AC2),
即(2AD)2+a2=2(b2+c2),
解得AD2=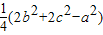 ,
,
故AD=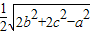 .
.
点评:此题主要考查学生对勾股定理,矩形的性质,平行四边形的性质和菱形的性质的理解和掌握,此题涉及到的知识点较多,综合性很强,有一定的拔高难度,属于难题.
(2)作AE⊥BC于点E,DF⊥BC交BC的延长线于F,再根据四边形ABCD是平行四边形,求证△ABE≌△DCF,得出AE=DF,BE=CF,由勾股定理得AC2=AE2+EC2=AE2+(BC-BE)2,BD2=DF2+BF2=DF2+(BC+CF)2=AE2+(BC+BE)2
(3)延长AD到E,使DE=AD,连接BE,CE,则AE=2AD,求证四边形ABEC是平行四边形,由(2)的结论,得AE2+BC2=2(AB2+AC2),解得AD2=
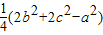 .
.解答:解:(1)如图2,设AC与BD相交于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,AC=2OA,BD=2OB.
在Rt△AOB中,由勾股定理,得
OA2+OB2=AB2,
∴AC2+BD2=4OA2+4OB2=4(OA2+OB2)=4AB2,
又∵AB=BC,
∴AC2+BD2=2(AB2+AB2)=2(AB2+BC2).
(2)小亮的猜想成立.
证明:作AE⊥BC于点E,DF⊥BC交BC的延长线于F,
则∠AEB=∠DFC=90°.
∵四边形ABCD是平行四边形,

∴AB=DC,AB∥CD,
∴∠ABE=∠DCF,
∴△ABE≌△DCF,
∴AE=DF,BE=CF.
在Rt△ACE和Rt△BDF中,由勾股定理,得
AC2=AE2+EC2=AE2+(BC-BE)2,
BD2=DF2+BF2=DF2+(BC+CF)2=AE2+(BC+BE)2,
∴AC2+BD2=2AE2+2BC2+2BE2=2(AE2+BE2)+2BC2.
又AE2+BE2=AB2,
故AC2+BD2=2(AB2+BC2).
(3)延长AD到E,使DE=AD,连接BE,CE,则AE=2AD.

∵BD=CD,
∴四边形ABEC是平行四边形.
由(2)的结论,得
AE2+BC2=2(AB2+AC2),
即(2AD)2+a2=2(b2+c2),
解得AD2=
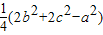 ,
,故AD=
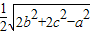 .
.点评:此题主要考查学生对勾股定理,矩形的性质,平行四边形的性质和菱形的性质的理解和掌握,此题涉及到的知识点较多,综合性很强,有一定的拔高难度,属于难题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目