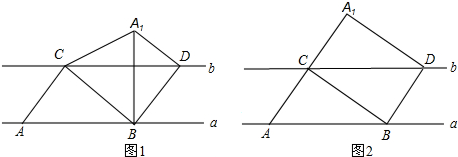��Ŀ����
��̽�����ε�����ʱ��С���õ���һ����Ȥ�Ľ��ۣ����������Խ��ߵ�ƽ���͵��������ߵ�ƽ���ͣ���ͼ1���ھ���ABCD�У��ɹ��ɶ�������AC2=AB2+BC2��BD2=AB2+AD2����CD=AB��AD=BC������AC2+BD2=AB2+BC2+CD2+AD2=2��AB2+BC2����С�������ν�����̽����Ҳ�õ���ͬ���Ľ��ۣ�����С�����룺����ƽ���ı��������Խ��ߵ�ƽ���͵��������ߵ�ƽ���ͣ��������������⣺
��1����ͼ2����֪���ı���ABCD�����Σ���֤��AC2+BD2=2��AB2+BC2����
��2������ΪС���IJ����Ƿ���������������������ͼ3����֤�����������������ٷ���˵����
��3����ͼ4���ڡ�ABC�У�BC��AC��AB�ij��ֱ�Ϊa��b��c��AD��BC���ϵ����ߣ�����AD�ij����������a��b��c��ʾ��

��������1����AC��BD�ཻ�ڵ�O�������ı���ABCD�����Σ��ó�AC=2OA��BD=2OB�����ù��ɶ�������OA2+OB2=AB2��������AB=BC��������֤AC2+BD2=2��AB2+BC2����
��2����AE��BC�ڵ�E��DF��BC��BC���ӳ�����F���ٸ����ı���ABCD��ƽ���ı��Σ���֤��ABE�ա�DCF���ó�AE=DF��BE=CF���ɹ��ɶ�����AC2=AE2+EC2=AE2+��BC-BE��2��BD2=DF2+BF2=DF2+��BC+CF��2=AE2+��BC+BE��2
��3���ӳ�AD��E��ʹDE=AD������BE��CE����AE=2AD����֤�ı���ABEC��ƽ���ı��Σ��ɣ�2���Ľ��ۣ���AE2+BC2=2��AB2+AC2�������AD2=
(2b2+2c2-a2)��
��2����AE��BC�ڵ�E��DF��BC��BC���ӳ�����F���ٸ����ı���ABCD��ƽ���ı��Σ���֤��ABE�ա�DCF���ó�AE=DF��BE=CF���ɹ��ɶ�����AC2=AE2+EC2=AE2+��BC-BE��2��BD2=DF2+BF2=DF2+��BC+CF��2=AE2+��BC+BE��2
��3���ӳ�AD��E��ʹDE=AD������BE��CE����AE=2AD����֤�ı���ABEC��ƽ���ı��Σ��ɣ�2���Ľ��ۣ���AE2+BC2=2��AB2+AC2�������AD2=
| 1 |
| 4 |
����⣺��1����ͼ2����AC��BD�ཻ�ڵ�O��
���ı���ABCD�����Σ�
��AC��BD��AC=2OA��BD=2OB��
��Rt��AOB�У��ɹ��ɶ�������
OA2+OB2=AB2��
��AC2+BD2=4OA2+4OB2=4��OA2+OB2��=4AB2��
�֡�AB=BC��
��AC2+BD2=2��AB2+AB2��=2��AB2+BC2����
��2�����IJ��������
֤������AE��BC�ڵ�E��DF��BC��BC���ӳ�����F��
���AEB=��DFC=90�㣮
���ı���ABCD��ƽ���ı��Σ�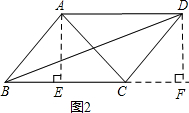
��AB=DC��AB��CD��
���ABE=��DCF��
���ABE�ա�DCF��
��AE=DF��BE=CF��
��Rt��ACE��Rt��BDF�У��ɹ��ɶ�������
AC2=AE2+EC2=AE2+��BC-BE��2��
BD2=DF2+BF2=DF2+��BC+CF��2=AE2+��BC+BE��2��
��AC2+BD2=2AE2+2BC2+2BE2=2��AE2+BE2��+2BC2��
��AE2+BE2=AB2��
��AC2+BD2=2��AB2+BC2����
��3���ӳ�AD��E��ʹDE=AD������BE��CE����AE=2AD��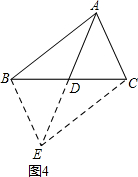
��BD=CD��
���ı���ABEC��ƽ���ı��Σ�
�ɣ�2���Ľ��ۣ���
AE2+BC2=2��AB2+AC2����
����2AD��2+a2=2��b2+c2����
���AD2=
(2b2+2c2-a2)��
��AD=
��
���ı���ABCD�����Σ�
��AC��BD��AC=2OA��BD=2OB��
��Rt��AOB�У��ɹ��ɶ�������
OA2+OB2=AB2��
��AC2+BD2=4OA2+4OB2=4��OA2+OB2��=4AB2��
�֡�AB=BC��
��AC2+BD2=2��AB2+AB2��=2��AB2+BC2����
��2�����IJ��������
֤������AE��BC�ڵ�E��DF��BC��BC���ӳ�����F��
���AEB=��DFC=90�㣮
���ı���ABCD��ƽ���ı��Σ�

��AB=DC��AB��CD��
���ABE=��DCF��
���ABE�ա�DCF��
��AE=DF��BE=CF��
��Rt��ACE��Rt��BDF�У��ɹ��ɶ�������
AC2=AE2+EC2=AE2+��BC-BE��2��
BD2=DF2+BF2=DF2+��BC+CF��2=AE2+��BC+BE��2��
��AC2+BD2=2AE2+2BC2+2BE2=2��AE2+BE2��+2BC2��
��AE2+BE2=AB2��
��AC2+BD2=2��AB2+BC2����
��3���ӳ�AD��E��ʹDE=AD������BE��CE����AE=2AD��

��BD=CD��
���ı���ABEC��ƽ���ı��Σ�
�ɣ�2���Ľ��ۣ���
AE2+BC2=2��AB2+AC2����
����2AD��2+a2=2��b2+c2����
���AD2=
| 1 |
| 4 |
��AD=
| 1 |
| 2 |
| 2b2+2c2-a2 |
������������Ҫ����ѧ���Թ��ɶ��������ε����ʣ�ƽ���ı��ε����ʺ����ε����ʵ���������գ������漰����֪ʶ��϶࣬�ۺ��Ժ�ǿ����һ���İθ��Ѷȣ��������⣮

��ϰ��ϵ�д�
 ��ʦ����ָ���ο�ʱϵ�д�
��ʦ����ָ���ο�ʱϵ�д�
�����Ŀ