摘要：多3.2岁.故选C．
网址：http://m.1010jiajiao.com/timu_id_428509[举报]
由2x+1＞42-x，得2x+1＞22（2-x），
解得x+1＞2（2-x），即x＞1，
所以a=2．
即方程（1-|2x-1|）=ax-1为（1-|2x-1|）=2x-1，
所以2-|2x-1|=2x，
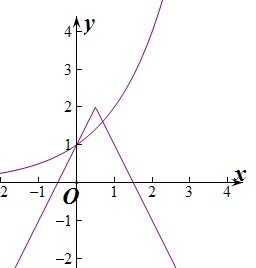
设y=2-|2x-1|，y=2x，
分别在坐标系中作出两个函数的图象，由图象可知两函数的交点个数为2个．
即方程（1-|2x-1|）=ax-1实数根的个数为2个．
故选C．
下列结论中，正确的是（ ）
①命题“如果p2+q2=2，则p+q≤2”的逆否命题是“如果p+q＞2，则p2+q2≠2”；
②已知
，
，
为非零的平面向量．甲：
•
=
•
，乙：
=
，则甲是乙的必要条件，但不是充分条件；
③p：y=a2（a＞0，且a≠1）是周期函数，q：y=sinx是周期函数，则p∧q是真命题；
④命题p：?x∈R，x2-3x+2≥0的否定是：￢P：?X∈R，x2-3x+2＜0．
①命题“如果p2+q2=2，则p+q≤2”的逆否命题是“如果p+q＞2，则p2+q2≠2”；
②已知
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| b |
| c |
③p：y=a2（a＞0，且a≠1）是周期函数，q：y=sinx是周期函数，则p∧q是真命题；
④命题p：?x∈R，x2-3x+2≥0的否定是：￢P：?X∈R，x2-3x+2＜0．
下面是一道选择题的两种解法，两种解法看似都对，可结果并不一致，问题出在哪儿？
[题]在△ABC中，a=x，b=2，B=45°，若△ABC有两解，则x的取值范围是（ ）
A．（2，+∞）B．（0，2）C.(2， 2
)D.(
， 2)
[解法1]△ABC有两解，asinB＜b＜a，xsin45°＜2＜x，即2＜x＜2
，故选C．
[解法2]
=
，sinA=
=
=
．
△ABC有两解，bsinA＜a＜b，2×
＜x＜2，即0＜x＜2，故选B．
你认为
查看习题详情和答案>>
[题]在△ABC中，a=x，b=2，B=45°，若△ABC有两解，则x的取值范围是（ ）
A．（2，+∞）B．（0，2）C.(2， 2
| 2 |
| 2 |
[解法1]△ABC有两解，asinB＜b＜a，xsin45°＜2＜x，即2＜x＜2
| 2 |
[解法2]
| a |
| sinA |
| b |
| sinB |
| asinB |
| b |
| xsin45° |
| 2 |
| ||
| 4 |
△ABC有两解，bsinA＜a＜b，2×
| ||
| 4 |
你认为
解法1
解法1
是正确的 （填“解法1”或“解法2”）
＝
＝
－ab，所以ab≤
，故B错；
＋
＝
＝
≥4，故A错；由基本不等式得
≤
＝
，即
＋
≤
，故C正确；a2＋b2＝(a＋b)2－2ab＝1－2ab≥1－2×