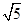摘要:=r(cos+isin).
网址:http://m.1010jiajiao.com/timu_id_425733[举报]
若把复数z=r(cosθ+isinθ)(i是虚数单位,r≥0)中的θ叫做复数z的幅角,比如复数z=1+i=
(cos
+isin
)的一个幅角为
,那么复数z0=
的一个幅角为( )
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| i |
阅读:设Z点的坐标(a,b),r=|
|,θ是以x轴的非负半轴为始边、以OZ所在的射线为终边的角,复数z=a+bi还可以表示为z=r(cosθ+isinθ),这个表达式叫做复数z的三角形式,其中,r叫做复数z的模,当r≠0时,θ叫做复数z的幅角,复数0的幅角是任意的,当0≤θ<2π时,θ叫做复数z的幅角主值,记作argz.
根据上面所给出的概念,请解决以下问题:
(1)设z=a+bi=r(cosθ+isinθ) (a、b∈R,r≥0),请写出复数的三角形式与代数形式相互之间的转换关系式;
(2)设z1=r1(cosθ1+isinθ1),z2=r2(cosθ2+isinθ2),探索三角形式下的复数乘法、除法的运算法则,请写出三角形式下的复数乘法、除法的运算法则.(结论不需要证明) 查看习题详情和答案>>
| OZ |
根据上面所给出的概念,请解决以下问题:
(1)设z=a+bi=r(cosθ+isinθ) (a、b∈R,r≥0),请写出复数的三角形式与代数形式相互之间的转换关系式;
(2)设z1=r1(cosθ1+isinθ1),z2=r2(cosθ2+isinθ2),探索三角形式下的复数乘法、除法的运算法则,请写出三角形式下的复数乘法、除法的运算法则.(结论不需要证明) 查看习题详情和答案>>
设复数z1=2sinθ+icosθ(<θ<
)在复平面上对应向量
,将
按顺时针方向旋转
π后得到向量
,
对应的复数为z2=r(cos∅+isin∅),则tg∅( )
| π |
| 2 |
| oz1 |
| oz1 |
| 3 |
| 4 |
| oz2 |
| oz2 |
| A、+12tgθ-1 | ||
B、
| ||
C、
| ||
D、
|
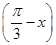 -cos
-cos (x∈R)的最小值等于( )
(x∈R)的最小值等于( )