题目内容
设复数z1=2sinθ+icosθ(<θ<
)在复平面上对应向量
,将
按顺时针方向旋转
π后得到向量
,
对应的复数为z2=r(cos∅+isin∅),则tg∅( )
| π |
| 2 |
| oz1 |
| oz1 |
| 3 |
| 4 |
| oz2 |
| oz2 |
| A、+12tgθ-1 | ||
B、
| ||
C、
| ||
D、
|
分析:先把复数z1 化为三角形式,再根据题中的条件求出复数z2,将求出的复数 z2和已知的复数 z2作对照,可得cos∅=cos(
π+β ),sin∅=sin(
π+β),可求tan∅,再把tanβ=
代入化简.
| 5 |
| 4 |
| 5 |
| 4 |
| cosθ |
| 2sinθ |
解答:解:∵复数z1=2sinθ+icosθ ( 0<θ<
) 的模为
=
,
∴复数z1=
(
+i
)=
(cosβ+i sinβ)
其中,cosβ=
,sinβ=
,β为锐角,∴tanβ=
,
∴z2 =
•(cos(β-
)+i sin(β-
))
=
•(cos(2π+β-
)+i sin(2π+β-
))=
•(cos(
π+β )+isin(
π+β)),
又已知复数 z2=r(cos∅+isin∅),∴cos∅=cos(
π+β ),sin∅=sin(
π+β),
∴tan∅=
=
=tan(
+β)=tan(
+β)=
=
=
=
,
故选 B.
| π |
| 2 |
| (2 sinθ)2+cos2θ |
| 1+3sin2θ |
∴复数z1=
| 1+3sin2θ |
| 2sinθ | ||
|
| cosθ | ||
|
| 1+3sin2θ |
其中,cosβ=
| 2sinθ | ||
|
| cosθ | ||
|
| cosθ |
| 2sinθ |
∴z2 =
| 1+3sin2θ |
| 3π |
| 4 |
| 3π |
| 4 |
=
| 1+3sin2θ |
| 3π |
| 4 |
| 3π |
| 4 |
| 1+3sin2θ |
| 5 |
| 4 |
| 5 |
| 4 |
又已知复数 z2=r(cos∅+isin∅),∴cos∅=cos(
| 5 |
| 4 |
| 5 |
| 4 |
∴tan∅=
| sin∅ |
| cos∅ |
sin(
| ||
cos(
|
| 5π |
| 4 |
| π |
| 4 |
| 1+tanβ |
| 1-tanβ |
1+
| ||
1-
|
| 2sinθ+cosθ |
| 2sinθ-cosθ |
=
| 2tanθ+1 |
| 2tanθ-1 |
故选 B.
点评:本题考查复数的三角形式,同角三角函数的基本关系、诱导公式的应用,以及利用棣莫弗定理进行复数三角形式的运算.

练习册系列答案
相关题目
 <θ<
<θ<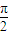 )在复平面上对应向量
)在复平面上对应向量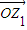 ,将
,将 按顺时针方向旋转
按顺时针方向旋转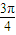 后得到向量
后得到向量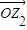 ,
,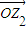 对应的复数为z2=r(cosφ+isinφ),则tanφ= .
对应的复数为z2=r(cosφ+isinφ),则tanφ= .