摘要：如图9―85.(Ⅰ)证明:因为A1B1C1―ABC是三棱柱.所以四边形B1BCC1是矩形.连B1C与BC1交于E.则E为B1C的中点.连DE.D是AC的中点.所以ED∥AB1.又ED平面BDC1.AB1平面BDC1.所以AB1∥平面BDC1.由已知平面ABC⊥平面BB1C1C.在平面ABC内作DF⊥BC.F为垂足.则DF⊥平面B1BCC1.连EF.EF为ED在平面B1BCC1上的射影.
网址：http://m.1010jiajiao.com/timu_id_425285[举报]
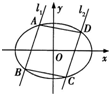（2012•海淀区一模）在平面直角坐标系xOy中，椭圆G的中心为坐标原点，左焦点为F1（-1，0），P为椭圆G的上顶点，且∠PF1O=45°．（Ⅰ）求椭圆G的标准方程；
（Ⅱ）已知直线l1：y=kx+m1与椭圆G交于A，B两点，直线l2：y=kx+m2（m1≠m2）与椭圆G交于C，D两点，且|AB|=|CD|，如图所示．（ⅰ）证明：m1+m2=0；（ⅱ）求四边形ABCD的面积S的最大值．
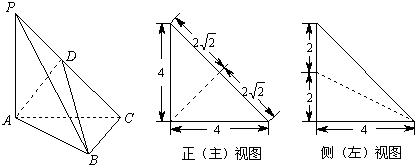
如图，在三棱锥P-ABC中，PA⊥平面ABC，AC⊥BC，D为侧棱PC上一点，它的正（主）视图和侧（左）视图如图所示．
（Ⅰ）证明：AD⊥平面PBC；
（Ⅱ）在∠ACB的平分线上确定一点Q，使得PQ∥平面ABD，并求此时PQ的长．
查看习题详情和答案>>
（Ⅰ）证明：AD⊥平面PBC；
（Ⅱ）在∠ACB的平分线上确定一点Q，使得PQ∥平面ABD，并求此时PQ的长．
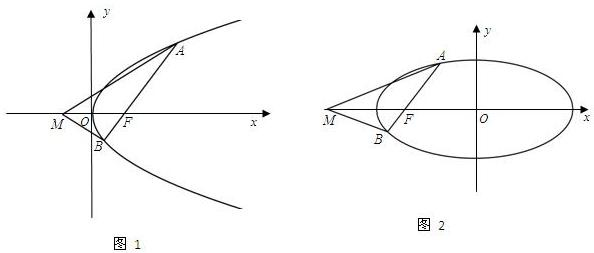
（1）如图1所示，请证明抛物线的一个几何性质：过抛物线y2=4x的焦点F任作直线l与抛物线交于A，B两点，则在x轴上存在定点M（-1，0），使直线MF始终是∠AMB的平分线；
（2）如图2所示，对于椭圆
+y2=1，设它的左焦点为F；请写出一个类似地性质；并证明其真假．
查看习题详情和答案>>
（2）如图2所示，对于椭圆
| x2 | 5 |
查看习题详情和答案>>
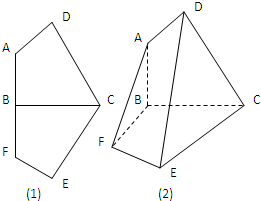（2012•安徽模拟）已知轴对称平面五边形ADCEF（如图1），BC为对称轴，ADCD，AD=AB=1，CD=BC=
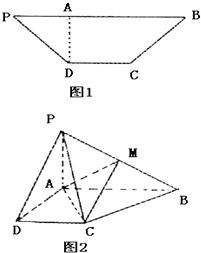已知等腰梯形PDCB中（如图1），PB=3，DC=1，PB=BC=