题目内容
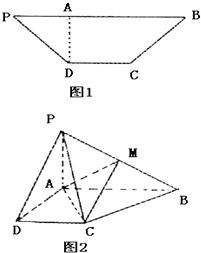 已知等腰梯形PDCB中(如图1),PB=3,DC=1,PB=BC=2a=|
已知等腰梯形PDCB中(如图1),PB=3,DC=1,PB=BC=2a=|| QP |
| QP′ |
(
|
(
|
| 10 |
(I)证明:平面PAD⊥PCD;
(II)试在棱PB上确定一点M,使截面AMC把几何体分成的两部分VPDCMA:VMACB=2:1;
(III)在M满足(Ⅱ)的情况下,判断直线AM是否平行面PCD.
分析:(I)由已知中CD⊥AD及面PAD⊥面ABCD,我们根据面面垂直的性质定理得到CD⊥平面PAD,再由面面垂直的判定定理得到平面PAD⊥PCD;
(II)根据(I)的结论,平面PAB⊥平面ABCD,在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD,利用体积公式,分别计算VPDCMA,VMACB,再根据VPDCMA:VMACB=2:1,即可求出满足条件的M为PB的中点;
(III)以A为原点,AD、AB、AP所在直线为x,y,z轴,建立如如图所示的空间直角坐标系,求出相关顶点的坐标,进而求出直线AM的方向向量及平面PCD的法向量,判定两个向量是否垂直,即可判断直线AM是否平行面PCD.
(II)根据(I)的结论,平面PAB⊥平面ABCD,在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD,利用体积公式,分别计算VPDCMA,VMACB,再根据VPDCMA:VMACB=2:1,即可求出满足条件的M为PB的中点;
(III)以A为原点,AD、AB、AP所在直线为x,y,z轴,建立如如图所示的空间直角坐标系,求出相关顶点的坐标,进而求出直线AM的方向向量及平面PCD的法向量,判定两个向量是否垂直,即可判断直线AM是否平行面PCD.
解答:解:(I)证明:依题意知:CD⊥AD.又∵面PAD⊥面ABCD∴DC⊥平面PAD.(2分)
∴平面PAD⊥PCD;
(II)由(I)知PA⊥平面ABCD
∴平面PAB⊥平面ABCD.(4分)
在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD,
设MN=h
则VM-ABC=
S△ABC•h=
×
×2×1×h=
VP-ABCD=
S△ABC•PA=
×
×1×1=
(6分)
要使VPDCMA:VMACB=2:1,即(
-
):
=2:1,解得h=
即M为PB的中点;
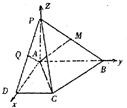 (III)以A为原点,AD、AB、AP所在直线为x,y,z轴,
(III)以A为原点,AD、AB、AP所在直线为x,y,z轴,
建立如如图所示的空间直角坐标系
则A(0,0,0),B(0,2,0),
C(1,1,0),D(1,0,0),
P(0,0,1),M(0,1,
)
由(I)知平面PAD⊥平面PCD,作AQ⊥PD,则AQ⊥平面PDC,则
为平面PCD的法向量.(10分)
又∵△PAD为等腰Rt△∴Q为PD的中点,即Q(
,0,
)
因为
•
=(
,0,
)(0,1,
)=
≠0,所以
不垂直
所以AM与平面PCD不平行.(13分)
∴平面PAD⊥PCD;
(II)由(I)知PA⊥平面ABCD
∴平面PAB⊥平面ABCD.(4分)
在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD,
设MN=h
则VM-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| h |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| (1+2) |
| 2 |
| 1 |
| 2 |
要使VPDCMA:VMACB=2:1,即(
| 1 |
| 2 |
| h |
| 3 |
| h |
| 3 |
| 1 |
| 2 |
即M为PB的中点;
 (III)以A为原点,AD、AB、AP所在直线为x,y,z轴,
(III)以A为原点,AD、AB、AP所在直线为x,y,z轴,建立如如图所示的空间直角坐标系
则A(0,0,0),B(0,2,0),
C(1,1,0),D(1,0,0),
P(0,0,1),M(0,1,
| 1 |
| 2 |
由(I)知平面PAD⊥平面PCD,作AQ⊥PD,则AQ⊥平面PDC,则
| AQ |
又∵△PAD为等腰Rt△∴Q为PD的中点,即Q(
| 1 |
| 2 |
| 1 |
| 2 |
因为
| AQ |
| AM |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| AQ |
| AM |
所以AM与平面PCD不平行.(13分)
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,熟练掌握空间直线、平面间平行与垂直的判定定理、性质定理、定义及几何特征是解答此类问题的关键.

练习册系列答案
相关题目
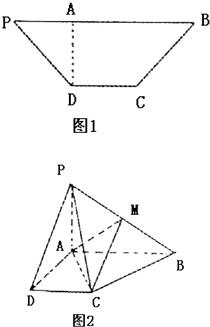 已知等腰梯形PDCB中(如图1),PB=3,DC=1,PD=BC=
已知等腰梯形PDCB中(如图1),PB=3,DC=1,PD=BC= 已知等腰梯形PDCB中,PB=3,DC=1,PD=
已知等腰梯形PDCB中,PB=3,DC=1,PD= (2008•盐城一模)已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=
(2008•盐城一模)已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=