题目内容
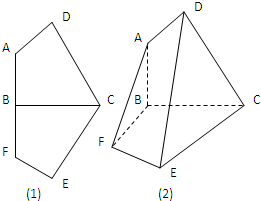 (2012•安徽模拟)已知轴对称平面五边形ADCEF(如图1),BC为对称轴,ADCD,AD=AB=1,CD=BC=
(2012•安徽模拟)已知轴对称平面五边形ADCEF(如图1),BC为对称轴,ADCD,AD=AB=1,CD=BC=| 3 |
图2)
(1)证明:AF∥平面DEC;
(2)求二面角E-AD-B的正切值.
分析:(1)先以B为坐标原点,分别以射线BF、BC、BA为x轴、y轴、z轴的正方向建立如图所示的坐标系.求出各点坐标以及
和
的坐标,进而得到两向量共线,即可证明线面平行.
(2)先根据条件求出两个半平面的法向量的坐标,进而求出二面角E-AD-B的余弦值,再结合同角三角函数之间的关系即可求出结论.
| AF |
| DE |
(2)先根据条件求出两个半平面的法向量的坐标,进而求出二面角E-AD-B的余弦值,再结合同角三角函数之间的关系即可求出结论.
解答: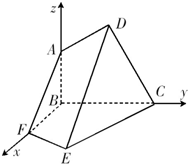 解:(1)以B为坐标原点,分别以射线BF、BC、BA为x轴、y轴、z轴的正方向建立如图所示的坐标系.
解:(1)以B为坐标原点,分别以射线BF、BC、BA为x轴、y轴、z轴的正方向建立如图所示的坐标系.
由已知与平面几何知识得,
A(0,0,1),F(1,0,0),D(0,
,
),E(
,
,0),
∴
=(1,0,-1),
=(
,0,-
),
∴
=
,∴AF∥DE,
又DE在平面DCE内,AF不在平面DEC内,
∴AF∥平面DEC…(6分)
(2)由(1)得A,D,E,F四点共面,
=(1,0,-1),AD=(0,
,
),
设
垂直于平面ADEF,
=(x,y,z),则
⇒
,
不妨令y=-1,故
=(
,-1,
),
由已知得平面ABCD的一个法向量为
=(1,0,0),
∴cos<
,
>=
=
=
=
,
设二面角E-AD-B的平面角为α
∴tanα=
=
=
.
∴二面角E-AD-B的正切值为
.…(12分)
 解:(1)以B为坐标原点,分别以射线BF、BC、BA为x轴、y轴、z轴的正方向建立如图所示的坐标系.
解:(1)以B为坐标原点,分别以射线BF、BC、BA为x轴、y轴、z轴的正方向建立如图所示的坐标系.由已知与平面几何知识得,
A(0,0,1),F(1,0,0),D(0,
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
∴
| AF |
| DE |
| 3 |
| 2 |
| 3 |
| 2 |
∴
| AF |
| 2 |
| 3 |
| DE |
又DE在平面DCE内,AF不在平面DEC内,
∴AF∥平面DEC…(6分)
(2)由(1)得A,D,E,F四点共面,
| AF |
| ||
| 2 |
| 1 |
| 2 |
设
| n |
| n |
|
|
不妨令y=-1,故
| n |
| 3 |
| 3 |
由已知得平面ABCD的一个法向量为
| m |
∴cos<
| n |
| m |
| ||||
|
|
| ||
|
| ||
|
| ||
| 7 |
设二面角E-AD-B的平面角为α
∴tanα=
|
|
2
| ||
| 3 |
∴二面角E-AD-B的正切值为
2
| ||
| 3 |
点评:本题主要考察用空间向量求平面间的夹角以及线面平行的证明.一般在证明线面平行时,常转化为证明线线平行.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目