摘要：∠PFE是二面角P―BC―D的平面角.在Rt△PEF中.tanPFE＝.所以∠PFE＝arctan.评述:本小题重点考查线面垂直.面面垂直.二面角及其平面角.棱锥的体积.在能力方面主要考查空间想象能力.
网址：http://m.1010jiajiao.com/timu_id_425284[举报]
如图，P是正方体ABCD-A1B1C1D1表面对角线A1C1上的一个动点，正方体的棱长为1．（1）求PA与DB所成角；
（2）求DC到面PAB距离d的取值范围；
（3）若二面角P-AB-D的平面角为α，二面角P-BC-D的平面角为β，求α+β的最小值．
如图所示，平面α内有一以AB为直径的圆，PA⊥α,点C在圆周上动（不与A、B重合），点D、E分别是A在PC、PB上的射影，下面结论:
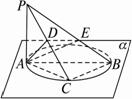
①∠AED是二面角A—PB—C的平面角;
②∠ACD是二面角P—BC—A的平面角;
③∠EDA是二面角A—PC—B的平面角;
④∠BAC是二面角B—PA—C的平面角;
⑤∠PAC是二面角P—AB—C的平面角.
其中正确结论的序号是____________________.
查看习题详情和答案>>
如图所示,平面α内有一以AB为直径的圆,PA⊥α,点C在圆周上移动(不与A、B重合),点D、E分别是A在PC、PB上的射影.有下面结论：
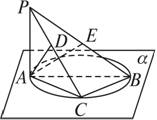
①∠AED是二面角A-PB-C的平面角；
②∠ACD是二面角P-BC-A的平面角；
③∠EDA是二面角A-PC-B的平面角；
④∠BAC是二面角B-PA-C的平面角；
⑤∠PAC是二面角P-AB-C的平面角.
其中正确结论的序号是__________.
查看习题详情和答案>>
如图，P是正方体ABCD-A1B1C1D1表面对角线A1C1上的一个动点，正方体的棱长为1．