题目内容
 如图,P是正方体ABCD-A1B1C1D1表面对角线A1C1上的一个动点,正方体的棱长为1.
如图,P是正方体ABCD-A1B1C1D1表面对角线A1C1上的一个动点,正方体的棱长为1.(1)求PA与DB所成角;
(2)求DC到面PAB距离d的取值范围;
(3)若二面角P-AB-D的平面角为α,二面角P-BC-D的平面角为β,求α+β的最小值.
分析:(1)利用线面垂直可知线线垂直,从而可求PA与DB所成角;
(2)由于DC∥面PAB,所以DC到面PAB距离d即为D到面PAB距离,故可求 DC到面PAB距离d的取值范围;
(3)先作出二面角的平面角,再利用和角三角函数计算即可.
(2)由于DC∥面PAB,所以DC到面PAB距离d即为D到面PAB距离,故可求 DC到面PAB距离d的取值范围;
(3)先作出二面角的平面角,再利用和角三角函数计算即可.
解答:解:(1)连接AC,BD,则BD⊥平面AC
∵PA?平面AC
∴PA⊥BD
∴PA与DB所成角为90°.
(2)由于DC∥面PAB
∴DC到面PAB距离d即为D到面PAB距离.
∵P是正方体ABCD-A1B1C1D1表面对角线A1C1上的一个动点
∴D到面PAB距离为 [
a,a]
(3)过P作PE⊥平面ABCD,过E分别作AB,BC的垂线,垂足分别为M,N,连PM,PN,则∠PME=α,∠PNE=β
设ME=x,NE=y,则tanα=
,tanβ=
∴tan(α+β)=
当且仅当x=y=
时,tan(α+β)=-
此时α+β的最小值为arctan(-
)
∵PA?平面AC
∴PA⊥BD
∴PA与DB所成角为90°.
(2)由于DC∥面PAB
∴DC到面PAB距离d即为D到面PAB距离.
∵P是正方体ABCD-A1B1C1D1表面对角线A1C1上的一个动点
∴D到面PAB距离为 [
| ||
| 3 |
(3)过P作PE⊥平面ABCD,过E分别作AB,BC的垂线,垂足分别为M,N,连PM,PN,则∠PME=α,∠PNE=β
设ME=x,NE=y,则tanα=
| 1 |
| x |
| 1 |
| y |
∴tan(α+β)=
| x+y |
| xy-1 |
当且仅当x=y=
| 1 |
| 2 |
| 4 |
| 3 |
此时α+β的最小值为arctan(-
| 4 |
| 3 |
点评:本题以正方体为载体,考查线线角,考查点、先面距离,考查面面角,有一定的综合性

练习册系列答案
相关题目
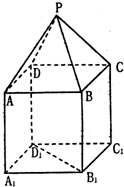 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=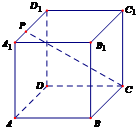 如图所示,已知点P是正方体ABCD-A1B1C1D1的棱A1D1上的一个动点,设异面直线AB与CP所成的角为α,则cosα的最小值是
如图所示,已知点P是正方体ABCD-A1B1C1D1的棱A1D1上的一个动点,设异面直线AB与CP所成的角为α,则cosα的最小值是 如图,P是正方体ABCD-A1B1C1D1表面对角线A1C1上的一个动点,正方体的棱长为1.
如图,P是正方体ABCD-A1B1C1D1表面对角线A1C1上的一个动点,正方体的棱长为1.