(1)解:如图9―83.连PD.由三垂线定理.PD⊥l.故∠ADP为二面角α―l―β的平面角.由PA＝AD得∠ADP＝45°,——青夏教育精英家教网——

摘要：(1)解:如图9―83.连PD.由三垂线定理.PD⊥l.故∠ADP为二面角α―l―β的平面角.由PA＝AD得∠ADP＝45°,

网址：http://m.1010jiajiao.com/timu_id_425267[举报]

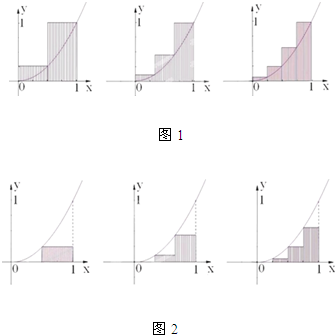为了求函数y=x²，函数x=1，x轴围成的曲边三角形的面积S，古人想出了两种方案求其近似解（如图）：第一次将区间[0，1]二等分，求出阴影部分矩形面积，记为S₂；第二次将区间[0，1]三等分，求出阴影部分矩形面积，记为S₃；第三次将区间[0，1]四等分，求出S₄…依此类推，记图1中S_n=a_n，图2中S_n=b_n，其中n≥2．
（1）求a₂，a₃，a₄；
（2）求a_n的通项公式，并证明an＞

；
（3）求b_n的通项公式，类比第②步，猜想b_n的取值范围．并由此推出S的值（只需直接写出b_n的范围与S的值，无须证明）．
参考公式：12+22+32+…+(n-1)2+n2=

n(n+1)(2n+1)．

查看习题详情和答案>>

（2013•泰安二模）已知数列a_n+1=a_n+na_n中，a₁=1，若利用如图所示的程序框图计算并输出该数列的第10项，则判断框内的条件可以是（　　）

查看习题详情和答案>>

A 若方程a^x-x-a=0有两个实数解，则a的取值范围是

B 如图，矩形ABCD中边长AB=2，BC=1，E为BC的中点，若F为正方形内（含边界）任意一点，则

的最大值为

查看习题详情和答案>>

已知函数y=f(x)的定义域是[-1，1]，其图像如图所示，则不等式-1≤f^-1（x）≤

的解集是( )

A．[-1，] B．[-2，]

C．[-2，0]∪ D．[-1，0]∪

查看习题详情和答案>>

已知函数y=f(x)的定义域为[-1，1]，其图像如图所示，则不等式-1≤f^-1(x)≤的解集是 ( )

A.[-1，] B.[-2，]

C.[-2，0)∪[，1) D.[-1，o)∪(，1]’

查看习题详情和答案>>