题目内容
 A 若方程ax-x-a=0有两个实数解,则a的取值范围是
A 若方程ax-x-a=0有两个实数解,则a的取值范围是(1,+∞)
(1,+∞)
B 如图,矩形ABCD中边长AB=2,BC=1,E为BC的中点,若F为正方形内(含边界)任意一点,则
| AE |
| AF |
| 9 |
| 2 |
| 9 |
| 2 |
分析:A:方程ax-x-a=0变形为:方程ax=x+a,由题意得,函数y=ax与函数y=a+x 有两个不同的交点,结合图象得出结果.
B:解:分别以AB为x轴,AD为y轴建立直角坐标系,则由E(2,
),C(2,1),设F(x,y)可求
•
=2x+
y,令z=2x+
y,则y=-4x+2z,2z为目标函数所对应的直线在y轴上的截距,截距越大,z越大,利用线性规划的知识可求
B:解:分别以AB为x轴,AD为y轴建立直角坐标系,则由E(2,
| 1 |
| 2 |
| AE |
| AF |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解A:方程ax-x-a=0变形为:方程ax=x+a,
由题意得,方程ax-x-a=0有两个不同的实数解,
即函数y=ax与函数y=a+x 有两个不同的交点,
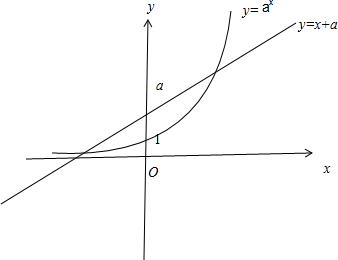
y=ax的图象过定点(0,1),直线y=x+a 的图象过定点(0,a),如图所示:
故直线y=x+a 在y轴上的截距大于1时,函数y=ax与函数y=a+x 有两个不同的交点
故答案为(1,+∞)
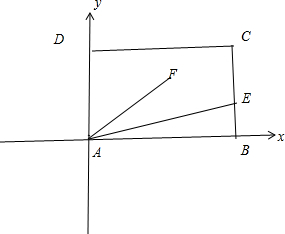
解B:分别以AB为x轴,AD为y轴建立直角坐标系,则E(2,
),C(2,1),设F(x,y)
∴
=(2,
),
=(x,y)
所以
•
=2x+
y
令z=2x+
y,则y=-4x+2z,2z为目标函数所对应的直线在y轴上的截距,截距越大,z越大
x,y满足的区域即矩形ABCD内及边界
结合线性规划的知识可得,当点F在C(2,1)处时,z最大,此时:z=2×2+
=
故答案为:
由题意得,方程ax-x-a=0有两个不同的实数解,
即函数y=ax与函数y=a+x 有两个不同的交点,
y=ax的图象过定点(0,1),直线y=x+a 的图象过定点(0,a),如图所示:
故直线y=x+a 在y轴上的截距大于1时,函数y=ax与函数y=a+x 有两个不同的交点
故答案为(1,+∞)

解B:分别以AB为x轴,AD为y轴建立直角坐标系,则E(2,
| 1 |
| 2 |
∴
| AE |
| 1 |
| 2 |
| AF |
所以
| AE |
| AF |
| 1 |
| 2 |
令z=2x+
| 1 |
| 2 |
x,y满足的区域即矩形ABCD内及边界
结合线性规划的知识可得,当点F在C(2,1)处时,z最大,此时:z=2×2+
| 1 |
| 2 |
| 9 |
| 2 |
故答案为:
| 9 |
| 2 |

点评:本题A主要考查了指数函数与一次函数的图象来解决方程根的问题,体现了数形结合思想的应用
B主要考查向量的数量积的应用,线性规划知识的应用,体现了转化与化规思想的应用.
B主要考查向量的数量积的应用,线性规划知识的应用,体现了转化与化规思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的最大值为 .
的最大值为 .