摘要：(Ⅱ)解:如图9―82.取AB中点G.连A1G.FG.因为F是CD中点.所以CFAD.又A1D1AD.所以GFA1D1.故GFD1A1是平行四边形.A1G∥D1F.设A1G与AE交于点H.则∠AHA1是AE与D1F所成的角.因E是BB1中点.所以Rt△A1AG≌Rt△ABE.∠GA1A＝∠GAH.从而∠AHA1＝90°.即直线AE与D1F所成角为直角.
网址：http://m.1010jiajiao.com/timu_id_425255[举报]
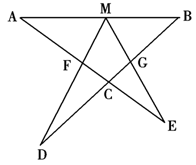
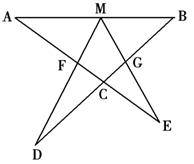
选修4-1：几何证明选讲如图设M为线段AB中点，AE与BD交于点C∠DME=∠A=∠B=α，且DM交AC于F，EM交BD于G．
（1）写出图中三对相似三角形，并对其中一对作出证明；
（2）连接FG，设α=45°，AB=4
| 2 |
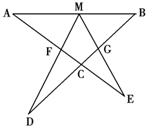
如图设M为线段AB中点，AE与BD交于点C ∠DME=∠A=∠B=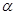
，且DM交AC于F，EM交BD于G。
（1）写出图中三对相似三角形，并对其中一对作出证明；
（2）连结FG，设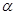=45°，AB=4
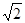，AF=3，求FG长。
查看习题详情和答案>>
选修4-1：几何证明选讲
如图设M为线段AB中点，AE与BD交于点C∠DME=∠A=∠B=α，且DM交AC于F，EM交BD于G．
（1）写出图中三对相似三角形，并对其中一对作出证明；
（2）连接FG，设α=45°，AB=4
，AF=3，求FG长．
查看习题详情和答案>>
如图设M为线段AB中点，AE与BD交于点C∠DME=∠A=∠B=α，且DM交AC于F，EM交BD于G．
（1）写出图中三对相似三角形，并对其中一对作出证明；
（2）连接FG，设α=45°，AB=4
，AF=3，求FG长．
查看习题详情和答案>>
，且DM交AC于F，EM交BD于G。
，AF=3，求FG长
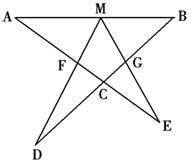
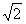，AF=3，求FG长。