题目内容
（选做题）如图设M为线段AB中点，AE与BD交于点C，∠DME=∠A=∠B=α，且DM交AC于F，EM交BD于G。
（1）写出图中三对相似三角形，并对其中一对作出证明；
（2）连结FG，设α=45°，AB=4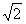
，AF=3，求FG长。
（1）写出图中三对相似三角形，并对其中一对作出证明；
（2）连结FG，设α=45°，AB=4
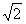，AF=3，求FG长。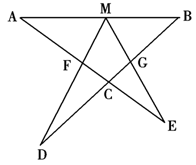
解：（1）△AME∽△MFE，△BMD∽△MGD，△AMF∽△BGM；
∵∠AMD=∠B+∠D，∠BGM=∠DMG+∠D，
又∠B=∠A=∠DME=α，
∴∠AMF=∠BGM，
∴△AMF∽△BGM。
（2）由（1）△AMF∽△BGM，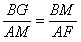
，
，
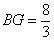∠α=45°，
∴△ABC为等腰直角三角形，
AB=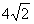
，AC=BC=4，CF=AC－AF=1，CG=4－
，
。
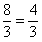∵∠AMD=∠B+∠D，∠BGM=∠DMG+∠D，
又∠B=∠A=∠DME=α，
∴∠AMF=∠BGM，
∴△AMF∽△BGM。
（2）由（1）△AMF∽△BGM，
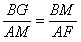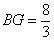，， ∠α=45°，
∴△ABC为等腰直角三角形，
AB=
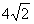，AC=BC=4，CF=AC－AF=1，CG=4－， 。
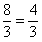练习册系列答案
小学教材完全解读系列答案
相关题目
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
，N＝
，设曲线y＝sinx在矩阵MN对应的变换作用下得到曲线F，求F的方程．
（t为参数）；在以O为极点、射线Ox为极轴的极坐标系中，曲线C的极坐标方程为ρsinθ＝8cosθ．若直线m与曲线C交于A、B两点，求线段AB的长．
≥2y＋3．