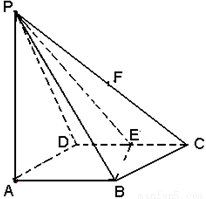
摘要:tanA1ED=.故∠A1ED=60°为所求.(Ⅲ)解法一:由点C作平面A1ABB1的垂线.垂足为H.则CH的长是C到平面A1ABB1的距离.连结HB.由于AB⊥BC.得AB⊥HB.又A1E⊥AB.知HB∥A1E.且BC∥ED.∴∠HBC=∠A1ED=60°.
网址:http://m.1010jiajiao.com/timu_id_425244[举报]
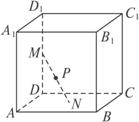
已知直平行六面体ABCD—A1B1C1D1的各条棱长均为3,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(08年长郡中学一模文)(12分)如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面![]() 内作菱形ABCD,边长为1,∠BAD=60°,再在面
内作菱形ABCD,边长为1,∠BAD=60°,再在面![]() 的上方,分别以△
的上方,分别以△![]() 与△
与△![]() 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
(Ⅰ)求证:PQ⊥BD;
(Ⅱ)求二面角P-BD-Q的余弦值;
(Ⅲ)求点P到平面QBD的距离;

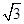 ,∠BCD=60°,则球O的表面积为
,∠BCD=60°,则球O的表面积为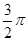 B.
B.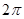 C.
C.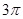 D.
D.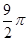
 ①
① ;
;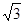 .
.